Forschung

Berechnung gebundener Zustände in der relativistischen Quantenmechanik

Forschungsartikel:

• Frank Rösler, Christiane Tretter; Computing Klein-Gordon Spectra, IMA Journal of Numerical Analysis, Band 45, Ausgabe 2, März 2025, Seiten 734-776.
  (unterstützt durch das Horizon 2020 Forschungs- und Innovationsprogramm der Europäischen Union im Rahmen des Marie Skłodowska-Curie-Stipendiums Nr. 885904.)
  (Eine Matlab-Implementierung des Algorithmus ist hier verfügbar.)

Überblick:

Das numerische Spektralproblem in der Quantenmechanik wird langsam immer besser verstanden. Insbesondere die numerische Komplexität der klassischen (nichtrelativistischen) Theorie, die auf Schrödinger und Heisenberg zurückgeht, wurde in verschiedenen Situationen von verschiedenen Autoren (darunter ich und meine Kooperationspartner) untersucht, siehe hier, hier oder hier. Für die relativistische Theorie, die sich mit Teilchen beschäftigt, deren Geschwindigkeit sich der Lichtgeschwindigkeit nähert, galt das bisher nicht. Die Grundlage der relativistischen Quantenmechanik bilden zwei Bewegungsgleichungen, die Dirac-Gleichung und die Klein-Gordon-Gleichung. Je nachdem, ob das betrachtete Teilchen Spin besitzt oder nicht, ersetzt eine dieser Gleichungen die klassische Schrödinger-Gleichung im relativistischen Rahmen.
Unsere obenstehende, kommende Forschungsarbeit beschäftigt sich mit der Berechnung der Eigenwerte der Klein-Gordon-Gleichung. Diese Gleichung beschreibt die Entwicklung relativistischer, spinloser Teilchen, am bekanntesten das Higgs-Boson, entdeckt durch die ATLAS- und CMS-Experimente am Large Hadron Collider (LHC) am CERN, wofür Peter Higgs und François Englert 2013 den Nobelpreis für Physik erhielten. Für ein Teilchen mit Masse $\mathsf{m}$ und Ladung $\mathsf{e}$, das mit einem elektrischen Feld $\mathsf{\varphi}$ wechselwirkt, lautet die Gleichung $$ \mathsf{\left( - \Bigl( -i \hbar\frac \partial {\partial t} - e \varphi \Bigr)^2 - \hbar^2c^2 \Delta + m^2c^4 \right) \psi = 0,} $$ wobei $\mathsf{c}$ die Lichtgeschwindigkeit und $\mathsf{\hbar}$ das Plancksche Wirkungsquantum bezeichnet. Trennt man die Zeitvariable durch $\mathsf{\psi(x,t) =: e^{i\lambda/\hbar t} u(x)}$ mit $\mathsf{x\in\mathbb R^d}$, $\mathsf{t\in\mathbb R}$, normiert $\mathsf{c}$ auf $\mathsf{1}$ und setzt $\mathsf{V}$ als den Multiplikationsoperator mit $\mathsf{e\varphi}$, so vereinfacht sich die Gleichung zu $$ \mathsf{(-\Delta+m^2)u = (V-\lambda)^2u. \tag{1}} $$ Die Lösung dieser Gleichung besteht darin, ein Paar $\mathsf{\lambda\in\mathbb C}$, $\mathsf{u\in L^2(\mathbb R^2)}$ zu finden, so dass $(1)$ erfüllt ist, wobei $\mathsf{V}$ eine bekannte Funktion ist. Dieses Problem erinnert an das Schrödinger-Eigenwertproblem, allerdings mit einem entscheidenden Unterschied: Die Potentialfunktion $\mathsf{V}$ und der spektrale Parameter $\mathsf{\lambda}$ treten quadratisch, statt linear auf! Dies macht das Problem nicht nur physikalisch, sondern auch mathematisch unklassisch: Man kann Ergebnisse der nichtrelativistischen Theorie nicht einfach übertragen, sondern benötigt neue Lösungsmethoden.

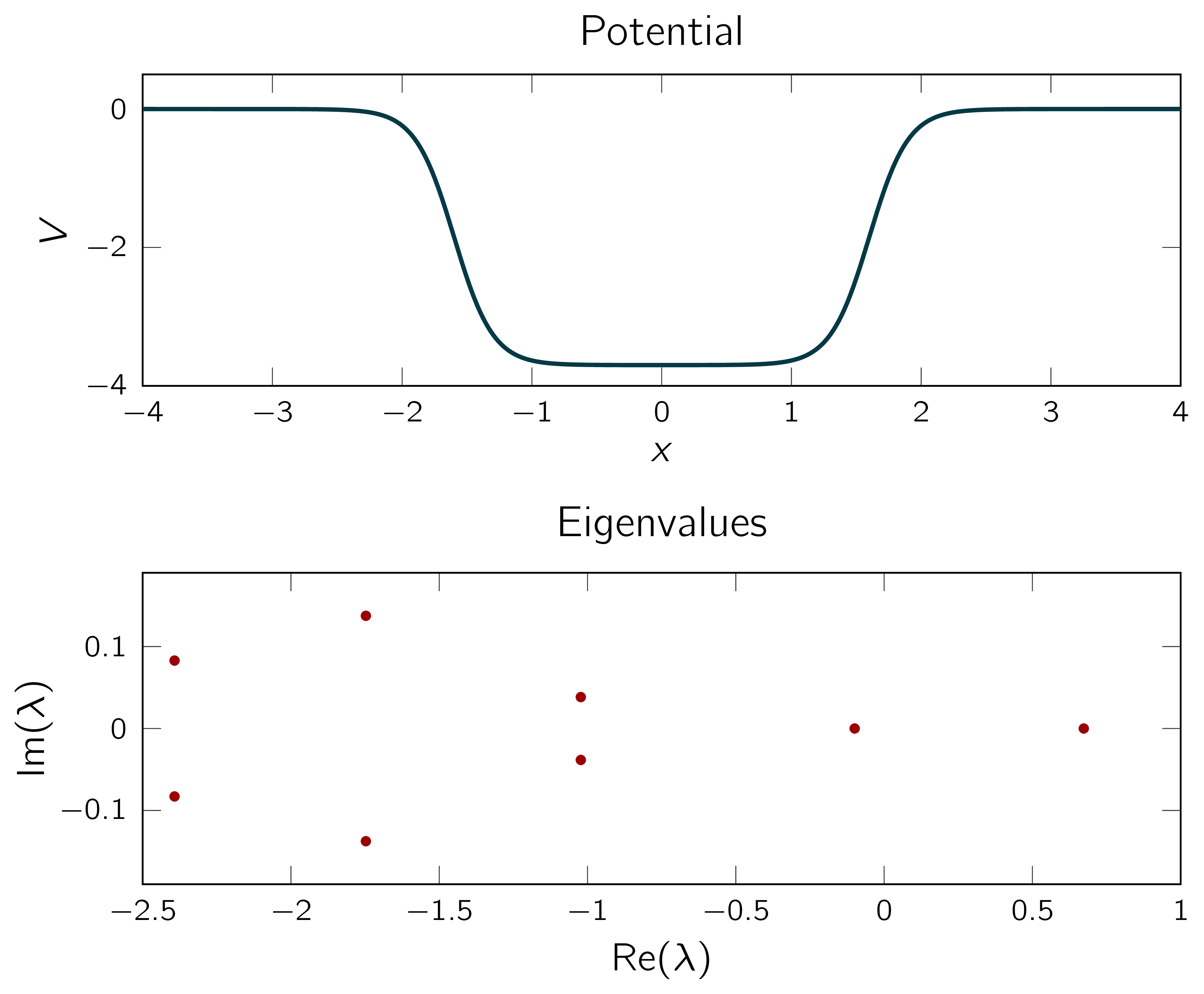
Wir entwickelten einen numerischen Algorithmus, basierend auf einem abstrakten, mathematischen Verständnis der Gleichung $(1)$, der automatisch die Eigenwerte $\lambda$ in der komplexen Ebene berechnet, gegeben eine Menge von Punktwerten $\mathsf{V(x)}$ des Potentials. Der Algorithmus kann auf einem Laptop implementiert und ausgeführt werden, und seine Ausgabe konvergiert garantiert zur korrekten Menge der Eigenwerte der Klein-Gordon-Gleichung. Die mathematische Strategie unseres Algorithmus besteht darin, einen Operator in Verbindung mit $\mathsf{(-\Delta+m^2)-(V-\lambda)^2}$ zu finden, der gut durch eine endlich-dimensionale Matrix $\mathsf{K(\lambda)}$ approximiert werden kann, und die approximativen Eigenwerte als Pole der Fredholm-Inversen $\mathsf{(I+K(\lambda))^{-1}}$ zu identifizieren. Die obige Abbildung zeigt das Ergebnis des Algorithmus für ein geglättetes Quadratpotential. Es liefert 8 approximative Eigenwerte in der komplexen Ebene, von denen 6 nicht-reell sind. Diese Nicht-Reellheit der Eigenwerte, selbst bei reellem Potential, ist ein wirklich relativistischer Effekt: Für die Schrödinger-Gleichung wäre dies unmöglich. In der Physik ist dies als der Schiff-Snyder-Weinberg-Effekt bekannt.