Forschung

Homogenisierung in perforierten Gebieten

Forschungsartikel:

Überblick:

Ein perforiertes Gebiet ist ein Gebiet, aus dem periodisch angeordnete Kugeln entfernt wurden, wobei sowohl der Abstand $\mathsf \epsilon$ als auch die Radien $\mathsf{r_\epsilon}$ der Kugeln viel kleiner als der Durchmesser des Gebiets sind, wie in der folgenden Abbildung dargestellt.

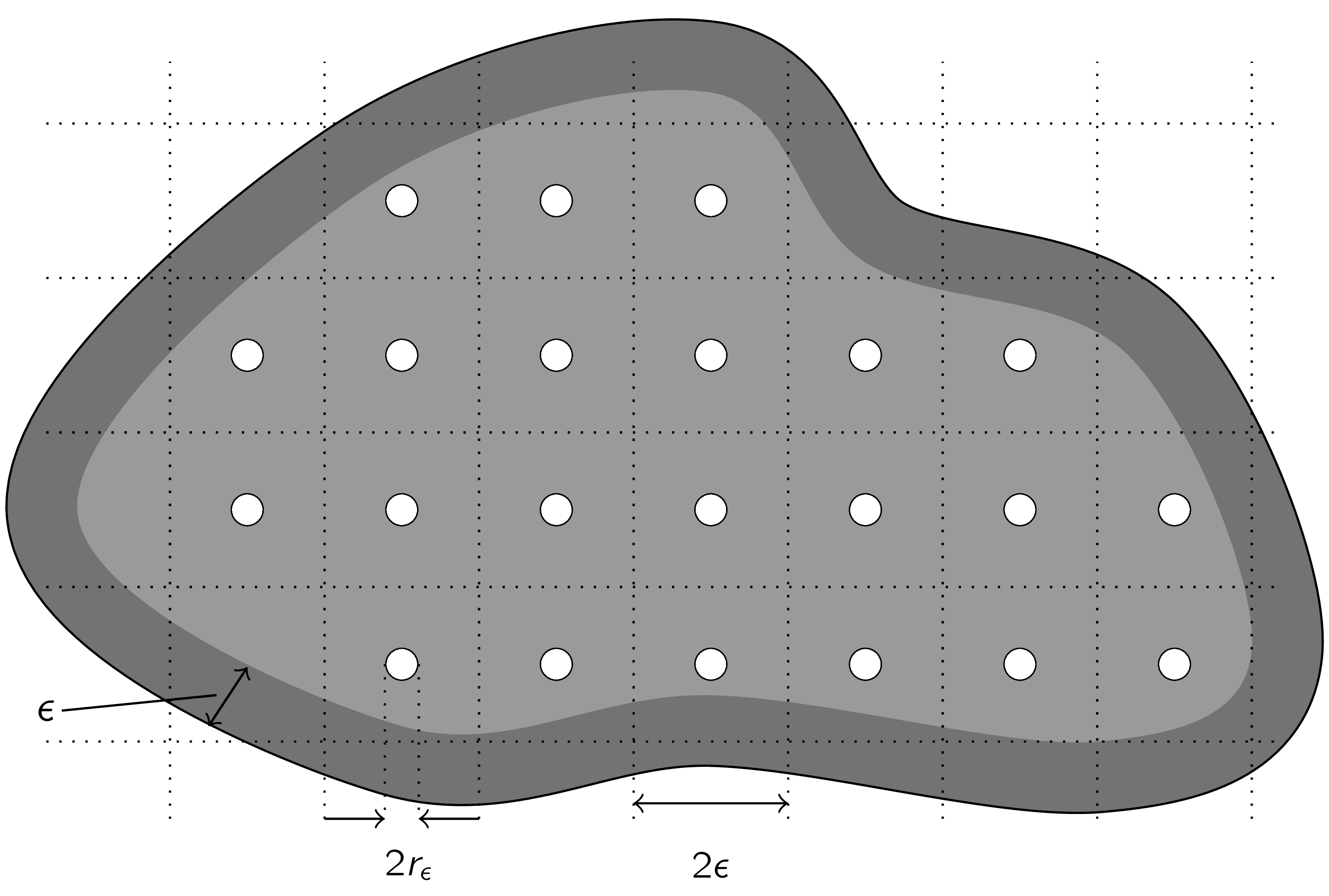
Diese Perforierung führt zu einem Gebiet $\mathsf{\Omega_\epsilon}$, auf dem eine partielle Differentialgleichung untersucht werden kann (je nach Gleichung modelliert dies Materialien mit feiner Mikrostruktur).
Es wurde gezeigt1, dass (vorausgesetzt die richtige Skalierung zwischen $\mathsf \epsilon$ und $\mathsf{r_\epsilon}$ gewählt wird) der Laplace-Operator einer Funktion $\mathsf{-\Delta_{\Omega_\epsilon} u}$ auf $\mathsf{\Omega_\epsilon}$ gegen einen Grenzwert konvergiert, der nicht einfach der Laplace-Operator auf dem ursprünglichen Gebiet $\mathsf{\Omega}$ ist, sondern eine verschobene Version $\mathsf{(-\Delta_\Omega + \mu)u}$, wobei $\mathsf\mu$ eine Konstante ist, die von der Größe der Löcher abhängt. Mehrere Autoren bezeichneten diese Konstante als „Ein seltsamer Term, der von nirgendwo kommt“2, da sie für jeden positiven Wert von $\mathsf\epsilon$ nicht vorhanden ist.

Während die Konvergenz $\mathsf{-\Delta_{\Omega_\epsilon} \to -\Delta_{\Omega}+\mu}$ für einzelne Funktionen bereits in den 1960er Jahren etabliert wurde, war die Frage, ob das Spektrum von $\mathsf{-\Delta_{\Omega_\epsilon}}$ gegen das Spektrum von $\mathsf{-\Delta_{\Omega}+\mu}$ konvergiert, bis zu unserem Beweis im oben genannten Artikel von 2018 offen. Tatsächlich zeigen wir nicht nur die Konvergenz der Spektren, sondern eine noch stärkere Aussage, die weitere Implikationen für das asymptotische Verhalten des zeitabhängigen Problems
$$\mathsf{\partial_t u(t,x) = \Delta u(t,x)}$$
auf perforierten Gebieten hat. Solche zeitabhängigen Gleichungen werden in Anwendungen zur Modellierung der Diffusion von Gasen und des Wärmetransports verwendet.

  1. [V. A. Marchenko & E. Ya. Khruslov. Randwertprobleme mit feinkörnigen Rändern [auf Russisch], Mat. Sb. (N.S.), 1964, Bd. 65(107), Nr. 3, 458-472] ↩︎

  2. [Cioranescu, Doina, und Francois Murat. A strange term coming from nowhere. Topics in the mathematical modelling of composite materials. Birkhäuser, Boston, MA, 1997. 45-93.] ↩︎