Forschung
Den Klang des Meeres in einer Muschel berechnen
Forschungsartikel:
- Jonathan Ben-Artzi, Marco Marletta, Frank Rösler; Computing the Sound of the Sea in a Seashell. Found. Comput. Math., 2021.
(unterstützt durch das Horizon 2020 Forschungs- und Innovationsprogramm der Europäischen Union im Rahmen des Marie Skłodowska-Curie-Stipendiums Nr. 885904.)
Hier klicken, um die Folien eines aktuellen Vortrags zu diesem Thema herunterzuladen. Ein Matlab-Paket basierend auf dem Artikel ist hier verfügbar.
Überblick:
In dieser Arbeit wird die Streuung von Wellen an Hindernissen in zwei Dimensionen untersucht. Die mathematische Grundlage für dieses Phänomen bildet der Laplace-Operator
$$
\mathsf{H = -\Delta \quad\textsf{ auf }\quad \mathbb R^2\setminus U,}
$$
wobei $\mathsf U$ das Hindernis bezeichnet und wir auf dem Rand von $\mathsf U$ Nullrandbedingungen annehmen.
Ist die räumliche Gestalt des Hindernisses so beschaffen, dass Wellen „fast eingeschlossen“ sind (z.B. wenn $\mathsf U$ die Form einer Kammer hat), beobachtet man das Phänomen langsam zerfallender Zustände (wie in meinem Artikel zu Quantenresonanzen beschrieben). Solche Streuresonanzen können mit denselben mathematischen Methoden wie Quantenresonanzen untersucht werden. Ein bekanntes Modellproblem mit Streuresonanzen ist der sogenannte Helmholtz-Resonator, definiert wie folgt:
Betrachte einen Bereich $\mathsf{U^\varepsilon\subset\mathbb R^2}$, der aus einer Kugel $\mathsf {B_r}$ besteht, die durch ein schmales Rohr mit Radius $\mathsf\varepsilon>0$ mit dem Außenraum $\mathsf{\mathbb R^2\setminus B_{R},;R>r}$ verbunden ist. Jede Welle, die in die Kammer eintritt, wird fast eingeschlossen, da Energie nur durch das Rohr entweichen kann.
Es wurde gezeigt, dass die Resonanzen dieses Problems Punkte in der komplexen Ebene sind, die bei $\mathsf{\varepsilon\to 0}$ gegen die Eigenwerte des Laplace-Operators auf der „geschlossenen“ Kammer $\mathsf {B_r}$ konvergieren.1

In unserem oben genannten Artikel entwickelten wir einen Algorithmus, der automatisch die Streuresonanzen von 2D-Hindernissen beliebiger Form berechnet. Die mathematische Idee des Algorithmus ist, die Resonanzen als Nullstellen einer analytischen Funktion, der sogenannten Dirichlet-zu-Neumann-Abbildung $\mathsf{M(k)}$, zu identifizieren. Diese Abbildung lässt sich durch eine $\mathsf{n\times n}$-Matrix vom Typ $\mathsf{I_n+K_n(k)}$ approximieren, wobei $\mathsf I$ die Einheitsmatrix ist und $\mathsf{K_n}$ eine konvergente Folge matrixwertiger Funktionen darstellt.
Die untenstehende Animation zeigt einen Konturplot der Funktion $\mathsf{\det(I_n+K_n(k))}$, berechnet in MATLAB. Die roten Punkte markieren die Eigenwerte des Laplace-Operators auf der Scheibe $\mathsf{B_r}$. Wie erwartet gibt es drei Nullstellen von $\mathsf{\det(I_n+K_n(k))}$ in der Nähe der drei roten Punkte, die mit wachsendem Öffnungsradius $\mathsf\varepsilon$ weiter nach unten in die komplexe Ebene wandern.
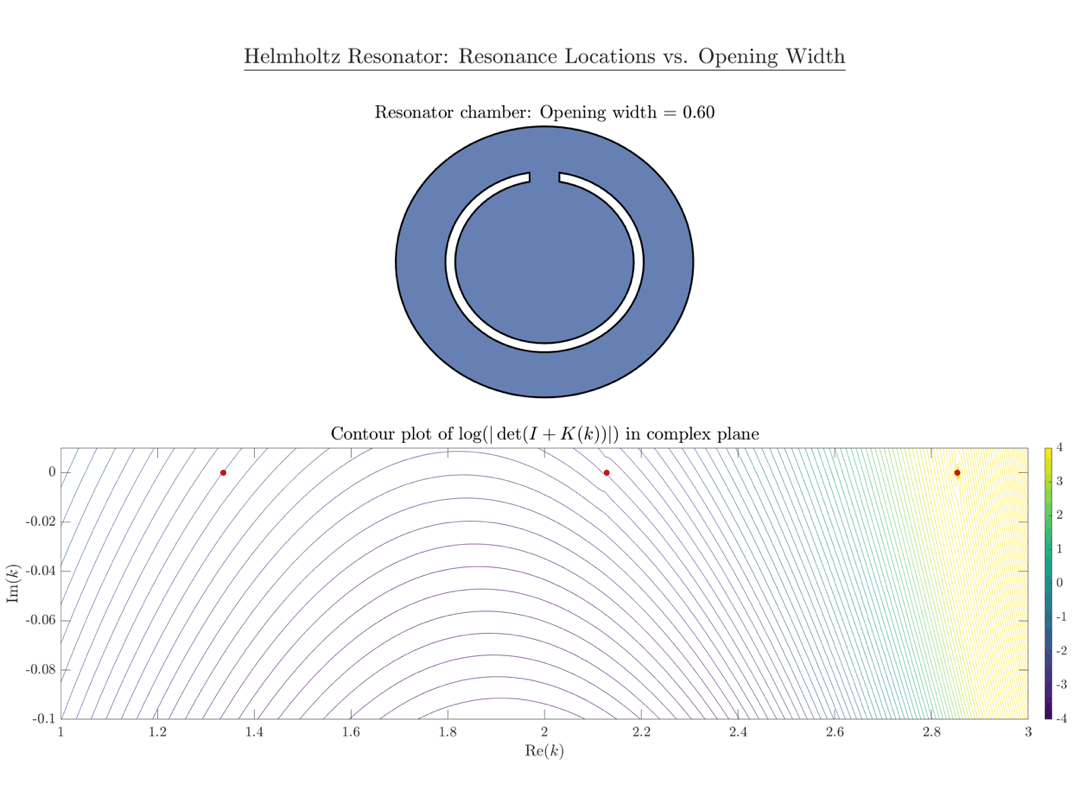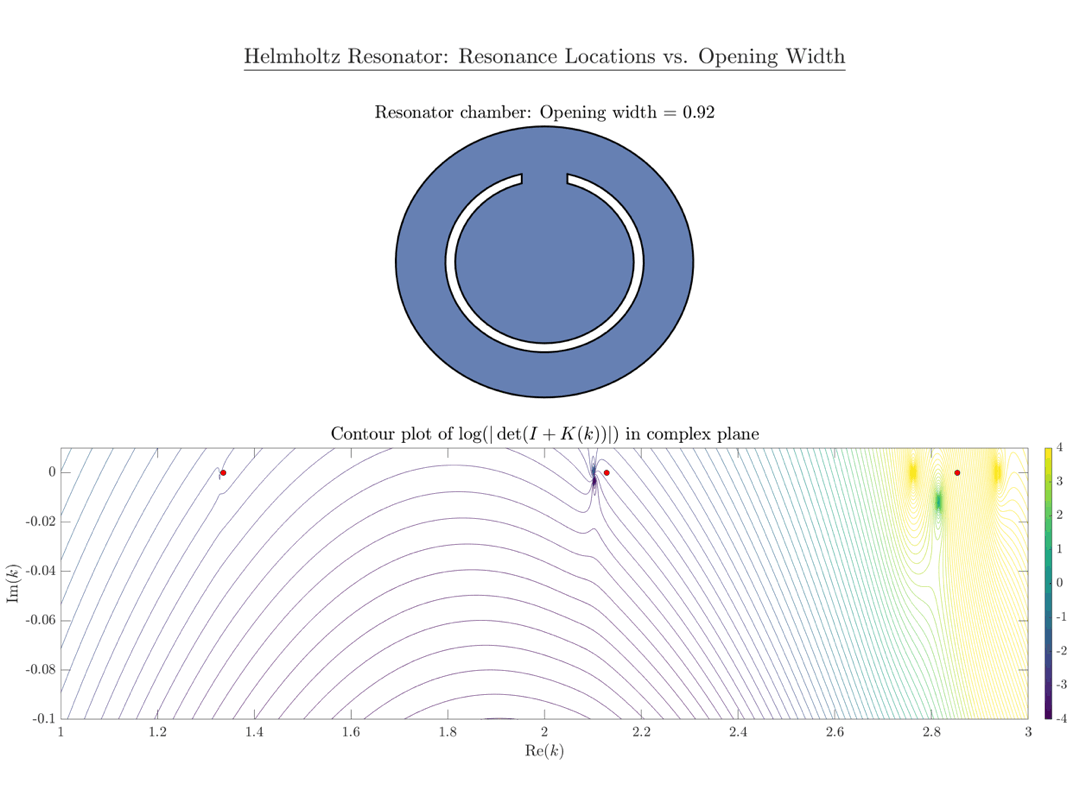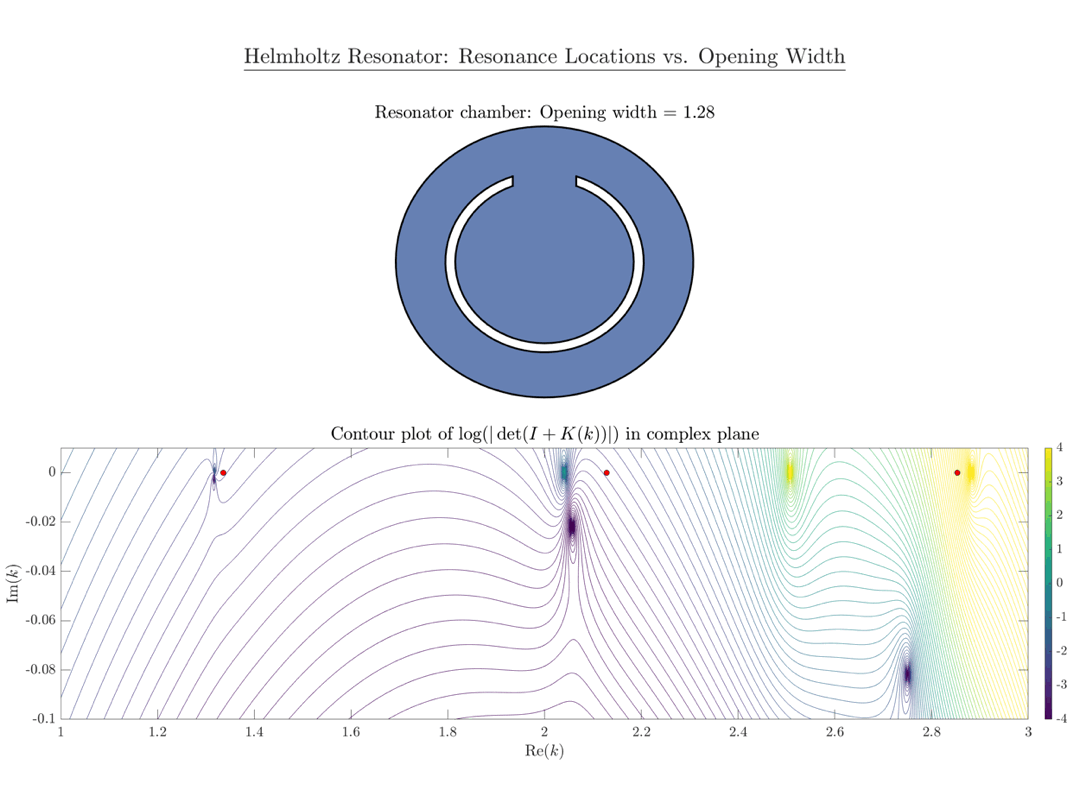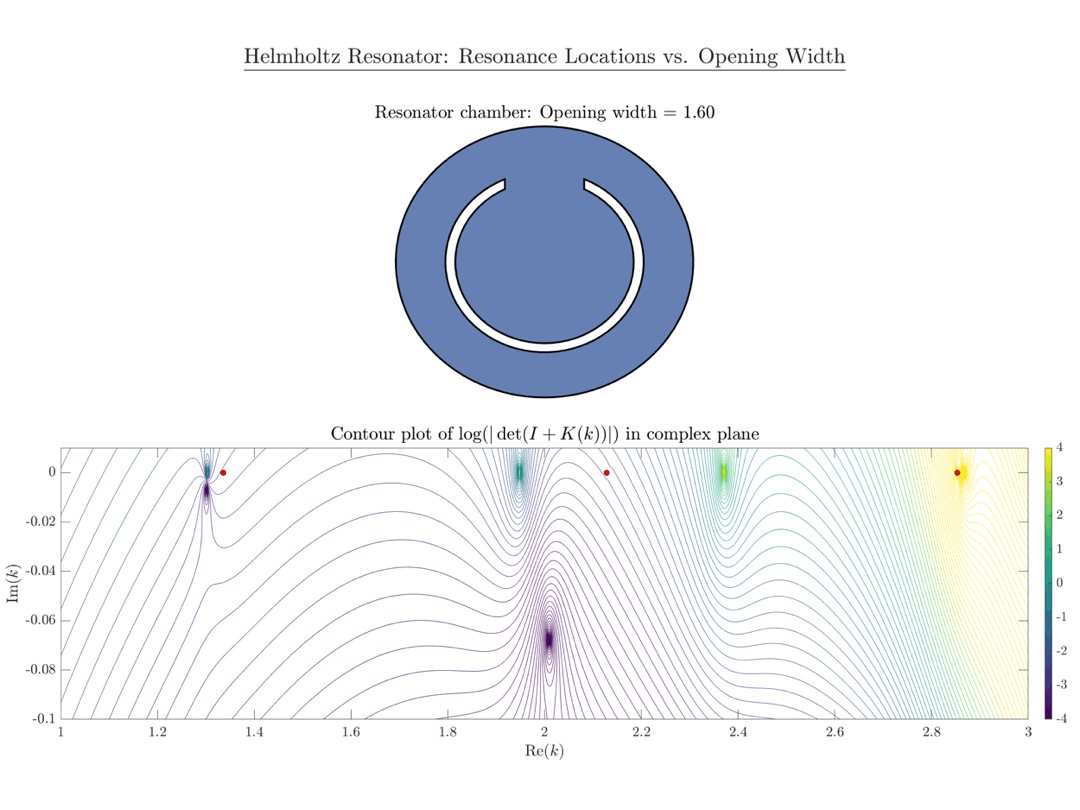
Eine MATLAB-Implementierung unserer Arbeit ist auf meiner GitHub-Seite verfügbar.
-
[Hislop, P. D., & Martinez, A. (1991). Scattering Resonances of a Helmholtz Resonator. Indiana Univ. Math. J., 767-788.] ↩︎