Forschung

Computational Quantum Mechanics

Forschungsartikel:

Überblick:

Diese Arbeit beschäftigt sich mit der numerischen Lösung des Eigenwertproblems der Schrödinger-Gleichung. Die Schrödinger-Gleichung steht im Zentrum der Quantenmechanik; ihre Eigenfunktionen und Eigenwerte beschreiben die gebundenen Zustände eines Quantensystems sowie deren Energieniveaus. In dimensionsloser Form lautet das Problem: Finde eine Funktion $\mathsf\psi$ und eine komplexe Zahl $\mathsf\lambda$, so dass $$ \mathsf{-\Delta \psi + V\psi = \lambda\psi} \tag{1} $$ gilt. Die skalare Funktion $\mathsf V$ beschreibt hierbei die potentielle Energie des Systems (z. B. verursacht durch ein elektrisches Feld, in dem sich das Teilchen bewegt). In den meisten praktischen Anwendungen ist eine analytische Lösung dieser Gleichung nicht möglich, sodass numerische Methoden erforderlich sind.

Für Potentiale, die glatt und reellwertig sind, existieren effiziente und weitgehend zuverlässige Verfahren (siehe jedoch das Problem der spectral pollution). Im Fall komplexwertiger Potentiale gestaltet sich das Eigenwertproblem jedoch deutlich schwieriger, und die Entwicklung robuster, zuverlässiger numerischer Algorithmen für eine breite Klasse solcher Potentiale stellt eine große Herausforderung dar.

In meinem oben genannten Artikel konstruiere ich einen neuen Algorithmus, der speziell auf diese Situation zugeschnitten ist. Das Verfahren konvergiert garantiert zur korrekten Lösung von (1), für beliebige Potentiale $\mathsf{V(x)}$, die für $\mathsf{|x|\to\infty}$ gegen 0 abfallen.

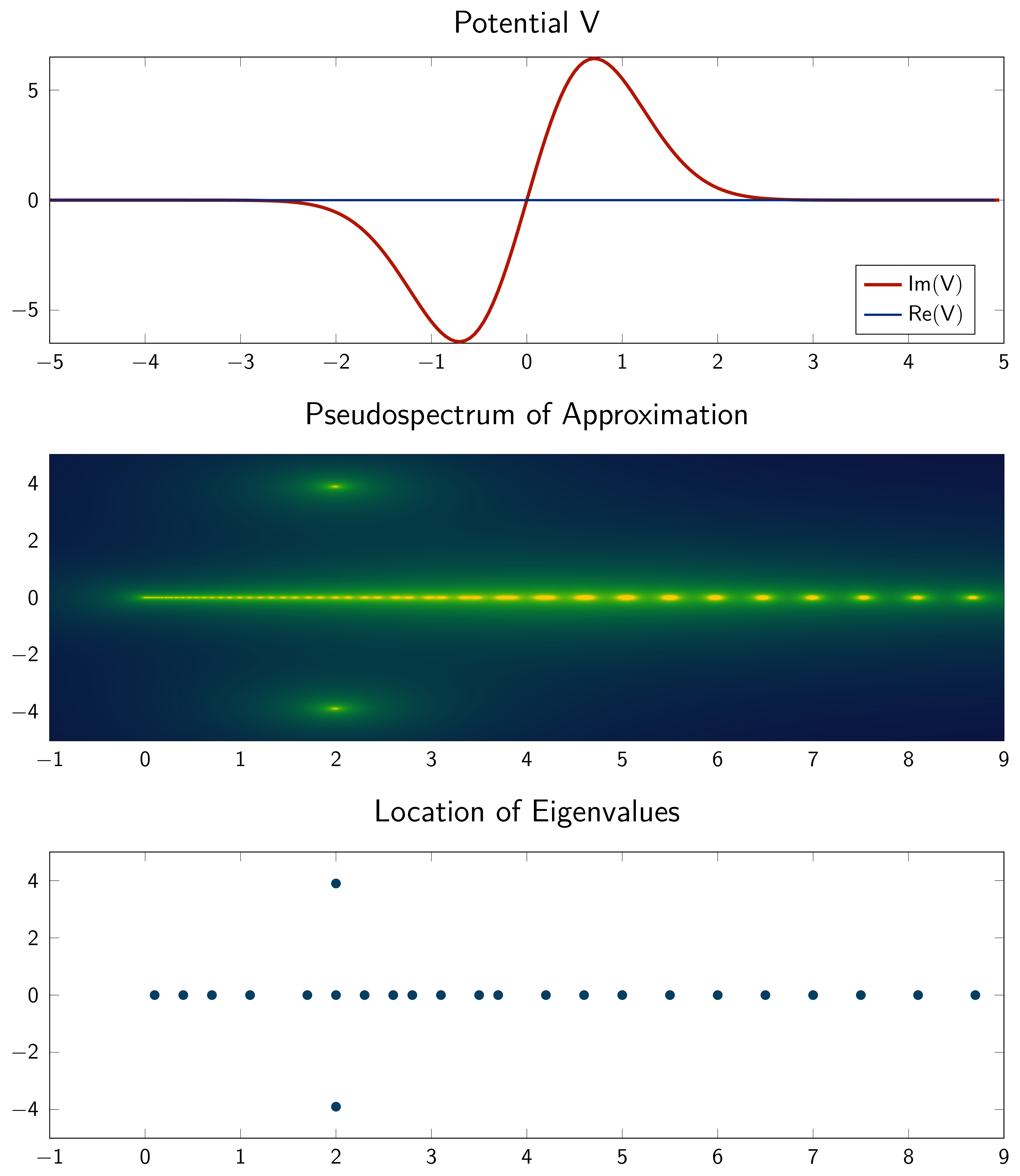
Die mathematische Idee hinter dem Algorithmus besteht darin, den Differentialoperator $\mathsf{-\Delta+V}$ durch eine Matrixapproximation zu ersetzen und dessen Pseudospektrum zu berechnen. Die Singularitäten dieses Pseudospektrums stimmen mit den Eigenwerten überein. Die Konvergenzbeweise nutzen den sogenannten essential numerical range, um spektrale Störungen (spectral pollution) zu kontrollieren.

Die obige Abbildung zeigt eine Beispielausgabe des Algorithmus (implementiert in MATLAB) für ein komplexwertiges Potential. Der Algorithmus approximiert sowohl das kontinuierliche Spektrum auf der positiven reellen Achse als auch zwei Eigenwerte bei ungefähr $\mathsf{2\pm 3.9i}$ korrekt.