Forschung

Pseudospektren nicht-hermitescher Hamiltonoperatoren

Forschungsartikel:

Überblick:

Dies war das erste Projekt meiner Promotion. Die Arbeit beschäftigt sich mit der Schrödinger-Gleichung mit komplexwertigen Potentialen. Im Allgemeinen kann das Spektrum (die Menge der Eigenwerte) solcher Operatoren irgendwo in der komplexen Ebene liegen. Es gibt jedoch Potentiale mit speziellen Symmetrien – sogenannte PT-Symmetrien – die ihre Eigenwerte auf die reelle Achse zwingen. Ein Beispiel ist der imaginäre kubische Oszillator, definiert durch $$ \mathsf{H = -\frac{d^2}{dx^2} + ix^3} \quad \textsf{ auf }\quad \mathsf{L^2(\mathbb R)} \tag{1} $$ Dieser Operator ist tatsächlich PT-symmetrisch, und es lässt sich zeigen, dass seine Eigenwerte rein reell sind, wie der folgende numerische Plot zeigt.

Operatoren wie $(1)$ sind von Interesse in der Theorie der nicht-hermiteschen Quantenmechanik1. Dieses Beispiel zeigt, dass man allein anhand des Spektrums eines Operators nicht entscheiden kann, ob sein Potential reell ist (d. h. ob der Operator selbstadjungiert ist). Dies motiviert die Einführung eines feineren Konzepts: des Pseudospektrums.

Das Pseudospektrum ist die Menge der Niveauflächen der Funktion $\mathsf{R(z) := |(H - z)^{-1}|}$. Es lässt sich zeigen, dass die Eigenwerte von $\mathsf{H}$ genau die Pole von $\mathsf{R(z)}$ sind. Für reellwertige Potentiale ist $\mathsf{R(z)}$ vollständig durch den Abstand von $\mathsf{z}$ zur Menge der Eigenwerte bestimmt (die Niveauflächen von $\mathsf{R(z)}$ sind dann Kreise um die Eigenwerte). Für nicht-reelle Potentiale hingegen kann das Pseudospektrum stark vom Spektrum abweichen.

Der folgende Plot zeigt eine Konturzeichnung von $\mathsf{R(z)}$ für den imaginären kubischen Oszillator $(1)$:

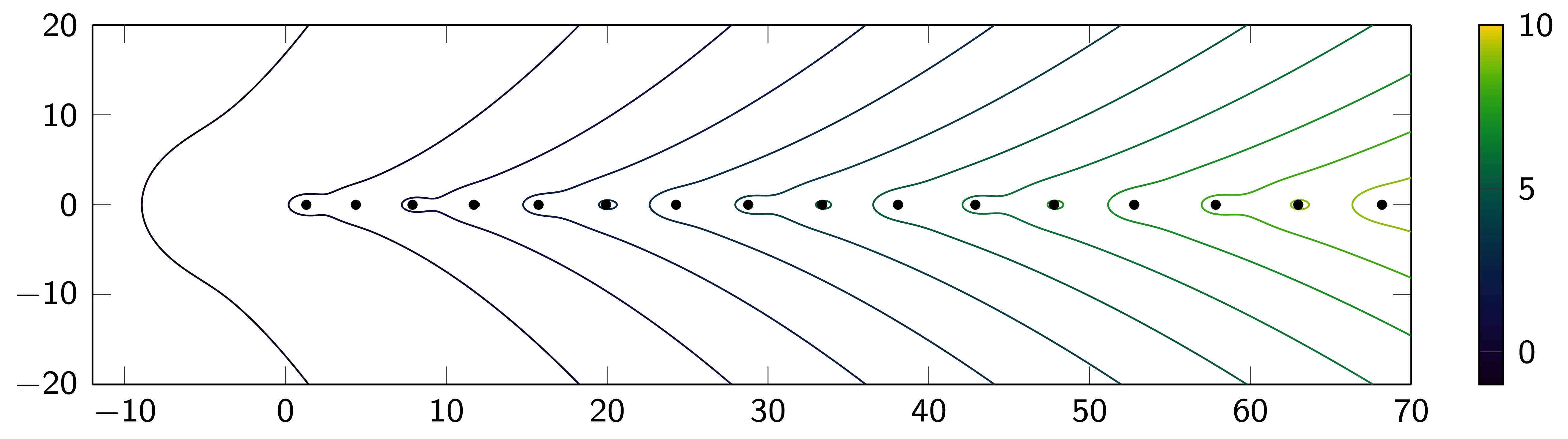
Wie man sieht, kann $\mathsf{R(z)}$ sehr große Werte annehmen – weit entfernt von den Eigenwerten. Ein solches Verhalten wäre für einen Hamiltonoperator mit reellwertigem Potential unmöglich.

Weitere Beispiele in der Literatur zeigen, dass das Pseudospektrum nicht-hermitescher Operatoren in der Tat beliebig chaotisch aussehen kann. Unser eigener Beitrag im oben genannten Artikel bestand darin, zu zeigen, dass für eine bestimmte Klasse von Operatoren – wie etwa den imaginären kubischen Oszillator – die Situation nicht völlig außer Kontrolle ist:

Auch wenn das Pseudospektrum nicht einfach durch den Abstand zum Spektrum gegeben ist, gelingt es uns, gewisse Schranken für $\mathsf{R(z)}$ herzuleiten. Diese zeigen, dass in jeder Halbebene, die sich nach links in die komplexe Ebene erstreckt, die Funktion $\mathsf{R(z)}$ bis zu einem gewissen Grad durch die Eigenwerte in dieser Halbebene bestimmt wird. Obwohl dies durch die obige Grafik nahegelegt wird, ist das mathematische Ergebnis keineswegs trivial und gilt nur für eine sehr eingeschränkte Klasse von Operatoren.

  1. [Bender, Carl M. Making sense of non-Hermitian Hamiltonians. Reports on Progress in Physics 70.6 (2007): 947.] ↩︎