Research
Quantum Resonances for Potential Scattering
Research article:
- Jonathan Ben-Artzi, Marco Marletta, and Frank Rösler. Computing scattering resonances. J. Eur. Math. Soc. (JEMS), 2022. (supported by the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement No 885904.) (A Matlab implementation of the algorithm is available here)
Overview:
Quantum resonances can be defined as states whose wave function disperses very slowly in time and can therefore be considered as “almost bound states”. In physics, such phenomena arise in the description of unstable particles and radioactive decay. Resonant states, just like eigenfunctions, can only exist at certain energies. Mathematically, a resonance energy can be defined as a local maximum of the spectral density function of the Hamiltonian.
Consider the Hamiltonian $\mathsf{H=-\frac{d^2}{dx^2}+q}$ on the half line $\mathbb R_+$ with boundary condition $\mathsf{\phi(0)=0}$. Via the Weyl-Kodaira formula, the spectral density $\mathsf\rho$ is related to the so-called Weyl solution $\mathsf\psi$ (which satisfies $\mathsf{(H-z^2)\psi=0}$ and $\mathsf{\psi(x,z)\sim e^{izx}}$ as $\mathsf{x\to\infty}$) by the formula $\mathsf{\pi\rho(z^2) = \frac{z}{|\psi(0,z)|^2}}$.
It can be shown that maxima of $\mathsf{\rho(z)}$ are the “imprints on the real axis” of poles of the analytic continuation of the function $\mathsf{\frac{z}{|\psi(0,z)|^2}}$ lying in the lower half plane. In the mathematical literature, the term “resonances” is often used to describe these poles, rather than the maxima of $\rho$.
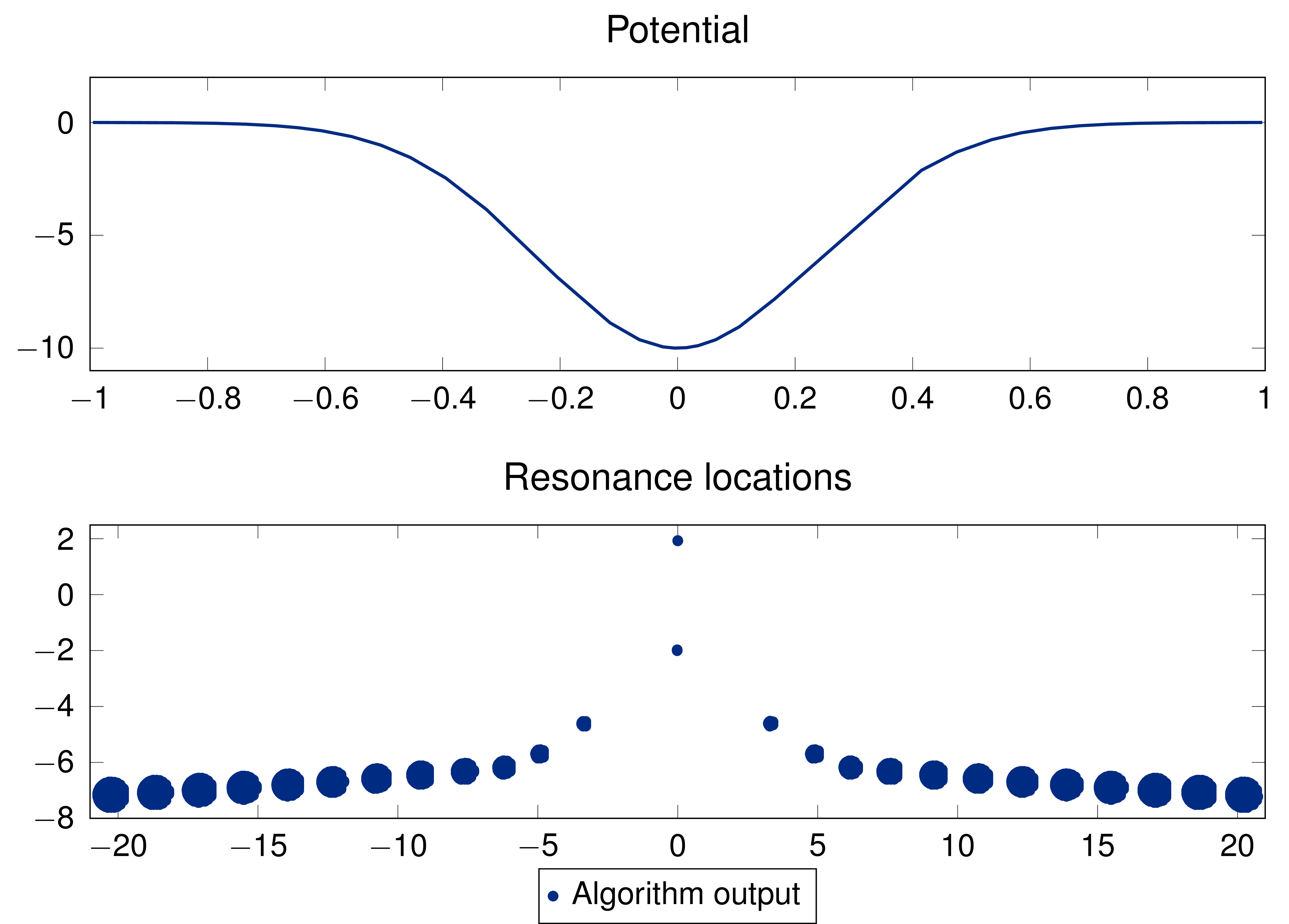
In the above research paper, we devised a numerical algorithm that, given a potential function $\mathsf q$, can compute the locations of its scattering resonances in the complex plane. The algorithm identifies the resonances as the poles of a certain nonnegative function on the complex plane, which can be computed algorithmically. An approximation of these zeros can thus be obtained by returning all points in the complex plane, where this function is larger than a given threshold value. This will yield a collection of small discs in the complex plane, in which the poles lie. The figure below shows the output of our algorithm for a Gaussian potential well.