Forschung

A Strange Vertex Condition Coming from Nowhere

Forschungsartikel:

Überblick:

Dies ist eine meiner Einzelautor-Publikationen im Bereich der asymptotischen Analysis. Der Artikel untersucht die kombinierte Wirkung zweier Eigenschaften einer Domäne: dünne Geometrie und Perforation.

Dünne Geometrie: Betrachte den Laplace-Operator $-\Delta$ auf einer Domäne $\mathsf{\Omega_\epsilon \subset \mathbb R^d}$, die im Limes $\mathsf{\epsilon \to 0}$ einen Graphen $\mathsf{\Gamma}$ approximiert.

Es lässt sich zeigen1, dass der Laplace-Operator auf $\mathsf{\Omega_\epsilon}$ im Grenzfall zu einem Operator auf dem Graphen konvergiert – mit bestimmten Sprungbedingungen an den Knotenpunkten, ähnlich den Kirchhoff-Bedingungen. Die genaue Form dieser Knotensprungbedingungen hängt vom relativen Skalierungsverhältnis der Kanten- und Knotenbereiche in $\mathsf{\Omega_\epsilon}$ ab.

Perforation: Eine perforierte Domäne ist ein Gebiet, aus dem eine regelmäßige Anordnung kleiner Kugeln entfernt wurde. Sowohl der Abstand $\mathsf{\epsilon}$ als auch die Radien $\mathsf{r_\epsilon}$ dieser Kugeln sind dabei sehr viel kleiner als der Gesamtdurchmesser der Domäne (mehr Details in diesem Post).

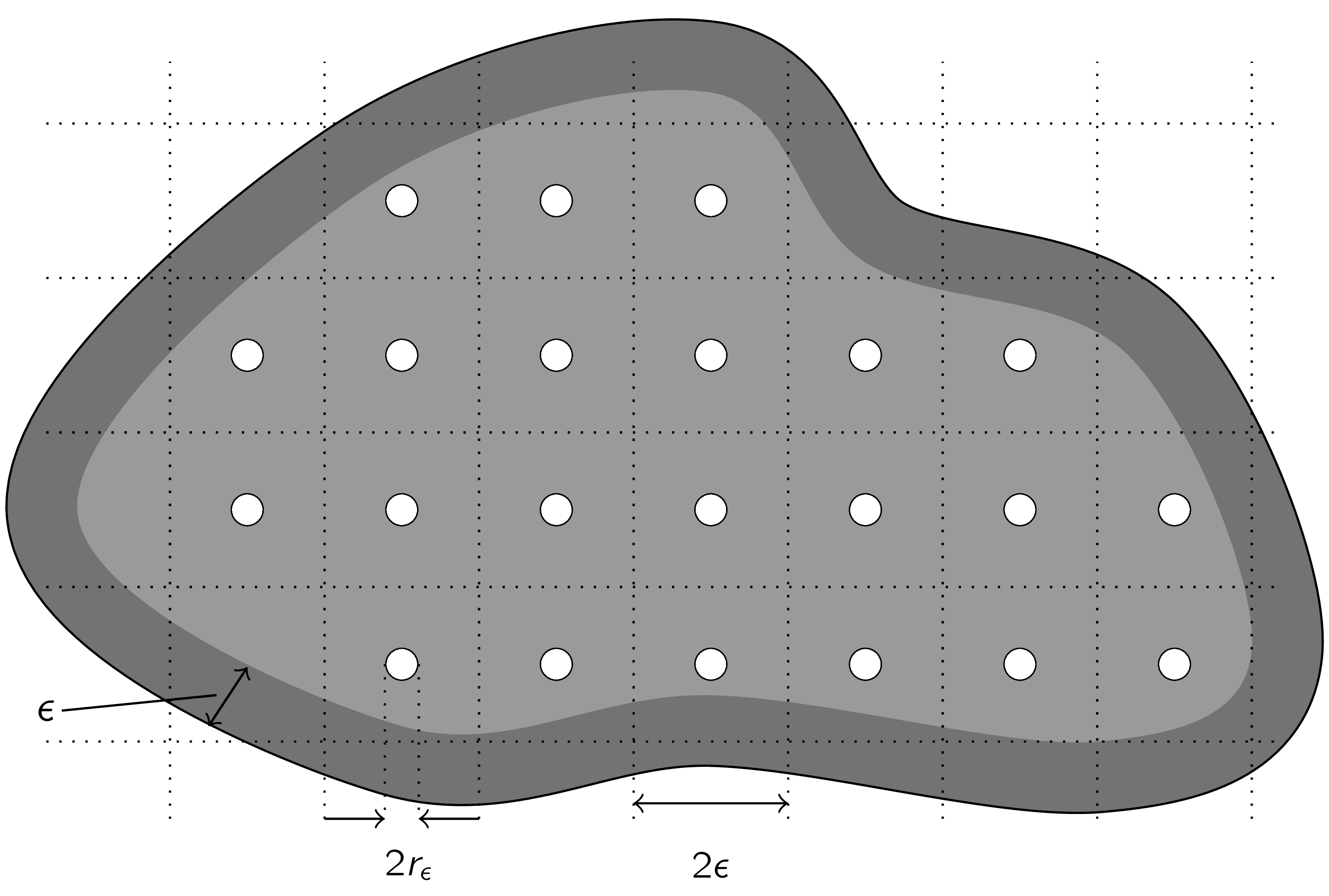
Die daraus resultierende Mikrostruktur beeinflusst die Lösung partieller Differentialgleichungen auf $\mathsf{\Omega_\epsilon}$. Es ist bekannt2, dass im Grenzfall $$ -\mathsf{\Delta_{\Omega_\epsilon} \to -\Delta_{\Omega} + \mu} \quad \text{für } \mathsf{\epsilon \to 0} $$ konvergiert, wobei $\mathsf{\mu}$ eine positive Konstante ist, die als der stracge term“ bezeichnet wird.

Kombination: In meinem Artikel habe ich die kombinierte Wirkung dünner, graphähnlicher Geometrie und feiner Perforation untersucht – also Domänen, die sowohl einen Graphen approximieren als auch stark perforiert sind.

Dabei ergibt sich eine bemerkenswerte Beobachtung: Wie im rein dünnen Fall lässt sich im Grenzfall ein Operator auf dem Graphen $\mathsf{\Gamma}$ finden. Auf jeder Kante wirkt dieser als verschobener zweiter Ableitungsoperator $\mathsf{-\frac{d^2}{dx^2} + \mu}$. Überraschend ist jedoch, dass der „seltsame Term“ $\mathsf{\mu}$ auch in den Knotensprungbedingungen des Grenzoperators auftaucht! Genauer gesagt lautet das Grenzproblem für die Gleichung $\mathsf{(-\Delta + z)u = f}$ auf $\mathsf{\Omega_\epsilon}$:

$$ \begin{cases} \mathsf{(-\Delta + z + \mu) u = f} &\text{auf } \mathsf{\Gamma} \\ \mathsf{\sum_{e \ni v} u'_e(v) = (z + \mu) \frac{|V|}{|\Omega_0|} u(v),} &\text{an jedem Knoten } \mathsf{v} \end{cases} $$

Das bedeutet: Der seltsame Term $\mu$, der die Dichte der Perforation beschreibt, beeinflusst nicht nur den Operator auf den Kanten, sondern auch direkt die Kopplungsbedingungen an den Knotenpunkten. Er kann somit als einstellbarer Parameter verwendet werden, um Kirchhoff-Bedingungen gezielt zu modifizieren.

  1. [P. Exner and O. Post. Convergence of spectra of graph-like thin manifolds. J. Geom. Phys. , 54(1) :77-115, 2005] ↩︎

  2. [Cioranescu, Doina, and Francois Murat. A strange term coming from nowhere. Topics in the mathematical modelling of composite materials. Birkhäuser, Boston, MA, 1997. 45-93.] ↩︎