Research

Computing Spectra of Periodic Operators

Research article:

  • Jonathan Ben-Artzi, Marco Marletta, Frank Rösler; Universal Algorithms for Computing Spectra of Periodic Operators, Numer. Math. (2022). ((supported by the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie grant agreement No 885904.)) A Matlab implementation of the algorithm is available here.

Overview:

Hamiltonians $\mathsf{H=-\Delta+V}$ with periodic potentials describe the movement of electrons in periodic media such as crystals. The spectra of Hamiltonians, which are periodic with respect to some lattice $\mathsf L$, are known to have a band structure, which provides a mathematical explanation for the existence of physical phenomena like conducting, insulating and semiconducting materials.
Their discrete analogues, which are obtained by replacing the derivatives in $\mathsf{-\Delta}$ by their finite difference approximations $\mathsf{\frac{\partial f(x)}{\partial x_i} \approx \frac{f(x+h_i)-f(x)}{h_i}}$, are of similar physical importance. Due to their discrete nature, such operators are generally more accessible for numerical algorithms than continuous operators. A notable physical application is the spectrum of graphene (a 2-dimensional material consisting of carbon atoms at the vertices of a hexagonal lattice) which has gained considerable attention in the analysis community in recent years. The general structure of periodic discrete Hamiltonians are infinite matrices of the form $$ \mathsf A = \begin{pmatrix} \ddots & \ddots & \ddots & & & & \\ & \mathsf{c_0} & \mathsf{a_0} & \mathsf{b_0} & & & \mathsf 0& & \\ & & \mathsf{c_1} & \mathsf{a_1} & \mathsf{b_1} & & & & \\ & & & \ddots & \ddots & \ddots & & & \\ & & & & \mathsf{c_{N-1}} & \mathsf{a_{N-1}} & \mathsf{b_{N-1}} & & \\ & &\mathsf 0 & & & \mathsf{c_0} & \mathsf{a_0} & \mathsf{b_0} & \\ & & & & & & \ddots & \ddots & \ddots \end{pmatrix} \tag{1} $$ In either case (continuous or discrete), the periodicity assumption allows to perform a Floquet-Bloch decomposition of the operator. That is, the Hamiltonian $\mathsf H$ can be represented as a direct integral over fibres $\mathsf{\widetilde H(\theta)}$ $$ \mathsf{H = \int^\oplus_{Q^*} \widetilde H(\theta),\mathrm{d}\theta,} $$ where $\mathsf{Q^*}$ is the fundamental cell of the dual lattice $\mathsf{L^*}$ and $\mathsf{\widetilde H(\theta)}$ are operators on $\mathsf{Q^*}$, which depend analytically on the parameter $\mathsf\theta$. It is well known that $\mathsf{\sigma(H)=\bigcup_{\theta\in Q^*}\sigma(\widetilde H(\theta))}$. Hence, the spectrum of $\mathsf H$ can be computed by computing the spectra of all $\mathsf{\widetilde H(\theta)}$ individually.
In the case of discrete Hamiltonians, the $\mathsf{\widetilde H(\theta)}$ are finite matrices, which vary continuously with $\mathsf\theta$. Accordingly, their spectra are given by a collection of one-parameter curves in the complex plane.
The following figure shows our numerical approximation of these curves for an operator of the form (1) with $$ \mathsf{(a_i) = (1, 0, 1, 0, 2)} $$ $$ \mathsf{(b_i) = (-1, -2, 1, 3\mathrm i, -5)} $$ $$ \mathsf{(c_i) = (2\mathrm i, -3\mathrm i, 2\mathrm i, 0, \mathrm i) }$$

In order to tackle the continuous problem numerically, a Fourier basis on $\mathsf{Q^*}$ can be used. This has the advantage that the matrix elements of $\mathsf{-\Delta}$ in this basis can be calculated explicitly. The matrix elements of the potential $\mathsf V$ can be computed via standard numerical quadrature schemes. Finally, the compactness of the resolvents of $\mathsf{\widetilde H(\theta)}$ can be used to prove that spectral pollution issues are absent and the procedure will yield the correct spectrum. The result will again be a subset of the complex plane, parameterised by $\mathsf\theta$, but in general this set will not be bounded. We implemented the numerical procedure described above in MATLAB, which yields an algorithm that can be applied to periodic potentials of arbitrary shape. As a case study, we considered the 1d operator $$\mathsf{H_\mu = -\frac{d^2}{dx^2} + \mu\cos(2\pi x),}$$ where $\mu$ can be any fixed complex number. One can prove theoretically that the spectrum of $\mathsf{H_q}$ always consists of a union of straight lines and arcs, as in the following figure.1
Below we show the output of our own algorithm, applied to the operator $\mathsf{H_\mu}$, for 3 different values of the parameter $\mathsf\mu$. Our results clearly exhibit the qualitative features from the figure above.

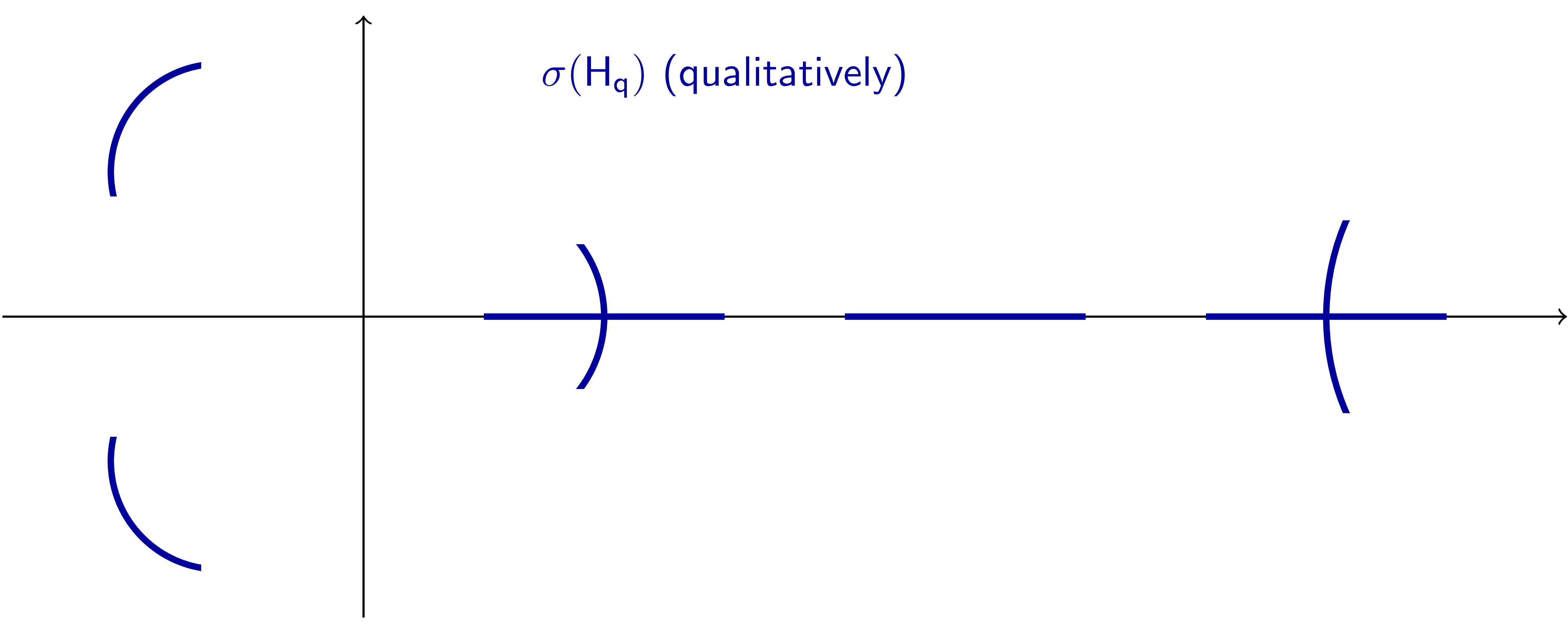
  1. [Shin. On the shape of spectra for non-self-adjoint periodic Schrodinger operators. J. Phys. A, 37(34):8287-8291, 2004] ↩︎