Forschung

Quantenresonanzen beim Potentialstreuungsproblem

Forschungsartikel:

• Jonathan Ben-Artzi, Marco Marletta und Frank Rösler. Computing scattering resonances. J. Eur. Math. Soc. (JEMS), 2022.
  (gefördert durch das Forschungs- und Innovationsprogramm Horizont 2020 der Europäischen Union im Rahmen des Marie Skłodowska-Curie-Stipendiums Nr. 885904)
  (Eine MATLAB-Implementierung des Algorithmus ist hier verfügbar)

Überblick:

Quantenresonanzen lassen sich als Zustände verstehen, deren Wellenfunktion sich nur sehr langsam über die Zeit zerstreut – sie können daher als „fast gebundene Zustände“ angesehen werden. Solche Phänomene treten in der Physik z. B. bei der Beschreibung instabiler Teilchen oder radioaktiven Zerfalls auf. Resonante Zustände existieren – wie Eigenfunktionen – nur bei bestimmten Energien.

Mathematisch lässt sich eine Resonanzenergie als lokales Maximum der Spektraldichtefunktion des Hamiltonoperators definieren.
Betrachte dazu den Hamiltonoperator $\mathsf{H = -\frac{d^2}{dx^2} + q}$ auf der Halbgeraden $\mathbb R_+$ mit der Randbedingung $\mathsf{\phi(0) = 0}$. Über die Weyl-Kodaira-Formel ist die Spektraldichte $\mathsf\rho$ mit der sogenannten Weyl-Lösung $\mathsf\psi$ verknüpft (diese erfüllt $\mathsf{(H - z^2)\psi = 0}$ und $\mathsf{\psi(x,z) \sim e^{izx}}$ für $\mathsf{x \to \infty}$) durch die Formel:
$$ \mathsf{\pi \rho(z^2) = \frac{z}{|\psi(0,z)|^2}}. $$

Es lässt sich zeigen, dass Maxima von $\mathsf{\rho(z)}$ „Abdrücke“ der Pole der analytischen Fortsetzung der Funktion $\mathsf{\frac{z}{|\psi(0,z)|^2}}$ sind – und zwar solcher Pole, die in der unteren Halbebene liegen. In der mathematischen Literatur bezeichnet man häufig diese Pole selbst als „Resonanzen“ (statt der Maxima der Spektraldichte).

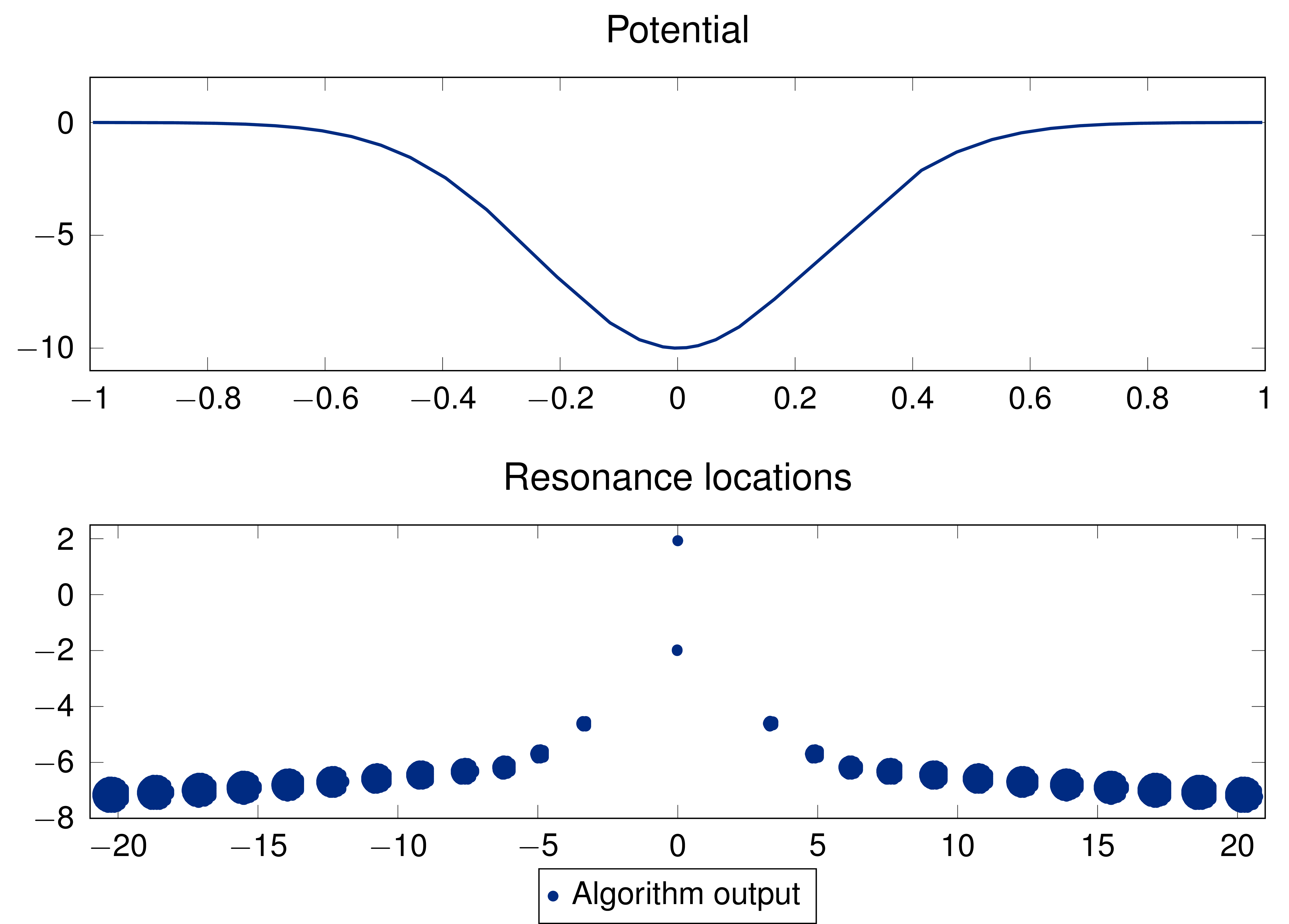
Im oben genannten Forschungsartikel haben wir einen numerischen Algorithmus entwickelt, der zu einem gegebenen Potential $\mathsf q$ die Positionen der Streuresonanzen in der komplexen Ebene berechnet. Der Algorithmus identifiziert die Resonanzen als Pole einer bestimmten nichtnegativen Funktion, die algorithmisch auf der komplexen Ebene berechnet werden kann.
Eine Approximation dieser Pole ergibt sich durch Rückgabe aller Punkte, an denen die Funktion einen gewissen Schwellwert überschreitet. Dies ergibt eine Sammlung kleiner Kreisscheiben in der komplexen Ebene, in denen die Resonanzen lokalisiert sind.

Die folgende Abbildung zeigt das Ergebnis unseres Algorithmus für ein gaußsches Potential: