Forschung
Spektren periodischer Operatoren berechnen
Forschungsartikel:
- Jonathan Ben-Artzi, Marco Marletta, Frank Rösler; Universal Algorithms for Computing Spectra of Periodic Operators, Numer. Math. (2022). (Gefördert durch das Horizon 2020 Forschungs- und Innovationsprogramm der Europäischen Union im Rahmen des Marie Skłodowska-Curie Stipendiums Nr. 885904.)
Eine Matlab-Implementierung des Algorithmus ist hier verfügbar.
Überblick:
Hamiltonoperatoren $\mathsf{H=-\Delta+V}$ mit periodischen Potentialen beschreiben die Bewegung von Elektronen in periodischen Medien wie Kristallen. Die Spektren solcher Hamiltonoperatoren, die bezüglich eines Gitters $\mathsf L$ periodisch sind, besitzen eine sogenannte Bandstruktur. Diese erklärt physikalische Phänomene wie leitende, isolierende und halbleitende Materialien mathematisch.
Die diskreten Analoga, die durch Ersetzen der Ableitungen in $\mathsf{-\Delta}$ durch endliche Differenzen $\mathsf{\frac{\partial f(x)}{\partial x_i} \approx \frac{f(x+h_i)-f(x)}{h_i}}$ entstehen, sind physikalisch ähnlich bedeutend. Aufgrund ihrer diskreten Natur sind sie für numerische Verfahren oft besser zugänglich als kontinuierliche Operatoren. Ein prominentes Beispiel ist das Spektrum von Graphen (einem zweidimensionalen Material mit Kohlenstoffatomen auf den Ecken eines hexagonalen Gitters), das in den letzten Jahren in der Analyse stark untersucht wurde. Die allgemeine Struktur periodischer diskreter Hamiltonoperatoren sind unendliche Matrizen der Form
$$
\mathsf
A = \begin{pmatrix} \ddots & \ddots & \ddots & & & & \\
& \mathsf{c_0} & \mathsf{a_0} & \mathsf{b_0} & & & \mathsf 0& & \\
& & \mathsf{c_1} & \mathsf{a_1} & \mathsf{b_1} & & & & \\
& & & \ddots & \ddots & \ddots & & & \\
& & & & \mathsf{c_{N-1}} & \mathsf{a_{N-1}} & \mathsf{b_{N-1}} & & \\
& &\mathsf 0 & & & \mathsf{c_0} & \mathsf{a_0} & \mathsf{b_0} & \\
& & & & & & \ddots & \ddots & \ddots
\end{pmatrix}
\tag{1}
$$
In beiden Fällen (kontinuierlich oder diskret) ermöglicht die Periodizitätsannahme eine Floquet-Bloch-Zerlegung des Operators. Das heißt, der Hamiltonoperator $\mathsf H$ kann als direktes Integral über Fasern $\mathsf{\widetilde H(\theta)}$ dargestellt werden
$$
\mathsf{H = \int^\oplus_{Q^*} \widetilde H(\theta),\mathrm{d}\theta,}
$$
wobei $\mathsf{Q^*}$ die Fundamentaleinheit des dualen Gitters $\mathsf{L^*}$ ist und $\mathsf{\widetilde H(\theta)}$ Operatoren auf $\mathsf{Q^*}$ sind, die analytisch vom Parameter $\mathsf\theta$ abhängen. Es ist wohlbekannt, dass $\mathsf{\sigma(H)=\bigcup_{\theta\in Q^*}\sigma(\widetilde H(\theta))}$. Das Spektrum von $\mathsf H$ kann somit durch die Spektren aller einzelnen $\mathsf{\widetilde H(\theta)}$ berechnet werden.
Bei diskreten Hamiltonoperatoren sind die $\mathsf{\widetilde H(\theta)}$ endliche Matrizen, die stetig von $\mathsf\theta$ abhängen. Dementsprechend bestehen ihre Spektren aus einer Sammlung von eindimensionalen Kurven in der komplexen Ebene.
Die folgende Abbildung zeigt unsere numerische Näherung dieser Kurven für einen Operator der Form (1) mit
$$ \mathsf{(a_i) = (1, 0, 1, 0, 2)} $$
$$ \mathsf{(b_i) = (-1, -2, 1, 3\mathrm i, -5)} $$
$$ \mathsf{(c_i) = (2\mathrm i, -3\mathrm i, 2\mathrm i, 0, \mathrm i) }$$

Zur numerischen Behandlung des kontinuierlichen Problems kann eine Fourierbasis auf $\mathsf{Q^*}$ verwendet werden. Das hat den Vorteil, dass die Matrixelemente von $\mathsf{-\Delta}$ in dieser Basis explizit berechnet werden können. Die Matrixelemente des Potentials $\mathsf V$ lassen sich mit Standardverfahren der numerischen Quadratur approximieren. Schließlich kann die Kompaktheit der Resolventen von $\mathsf{\widetilde H(\theta)}$ genutzt werden, um zu zeigen, dass keine spectral pollution auftritt und das Verfahren das korrekte Spektrum liefert. Das Ergebnis ist erneut eine Teilmenge der komplexen Ebene, parametrisiert durch $\mathsf\theta$, die aber im Allgemeinen unbeschränkt sein kann. Wir haben das beschriebene numerische Verfahren in MATLAB implementiert, was einen Algorithmus ergibt, der auf periodische Potentiale beliebiger Form anwendbar ist.
Als Anwendungsbeispiel haben wir den eindimensionalen Operator
$$\mathsf{H_\mu = -\frac{d^2}{dx^2} + \mu\cos(2\pi x),}$$
betrachtet, wobei $\mu$ eine beliebige komplexe Zahl sein kann. Es lässt sich theoretisch beweisen, dass das Spektrum von $\mathsf{H_\mu}$ stets aus einer Vereinigung von Geraden und Bögen besteht, wie in der folgenden Abbildung dargestellt.1
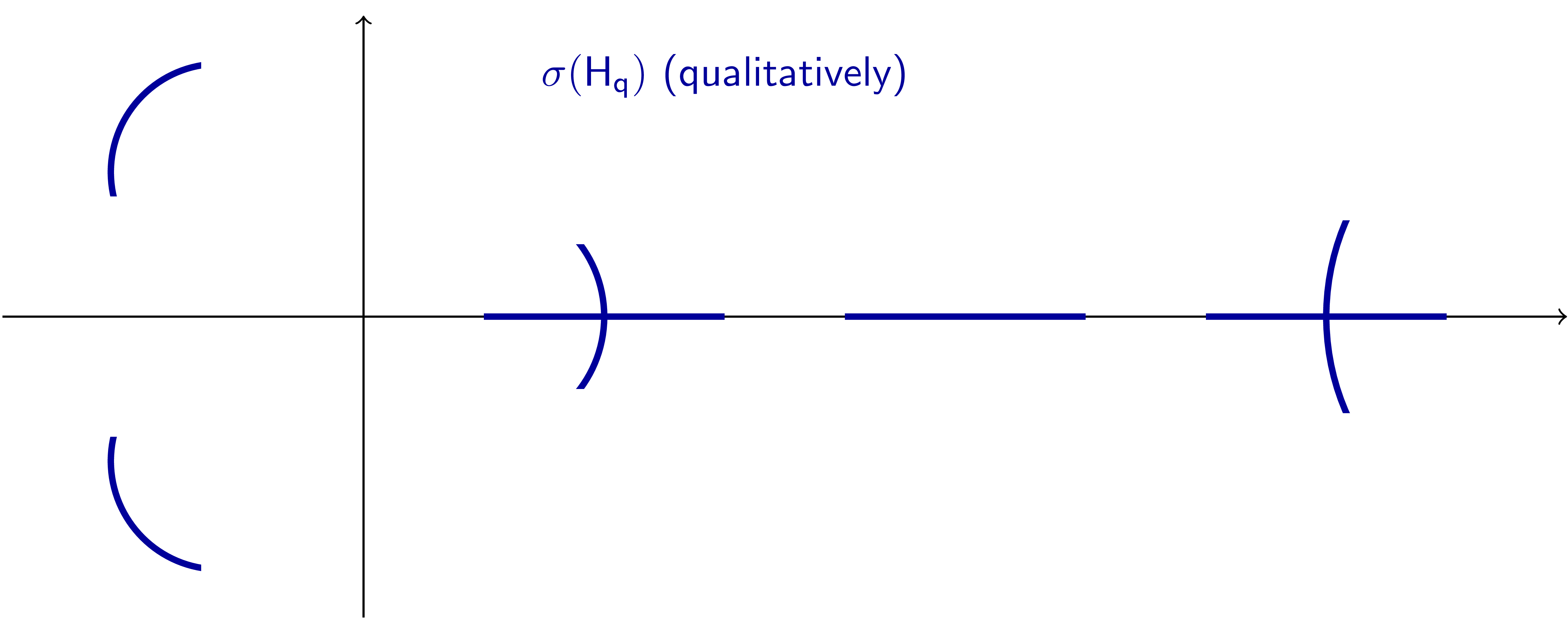
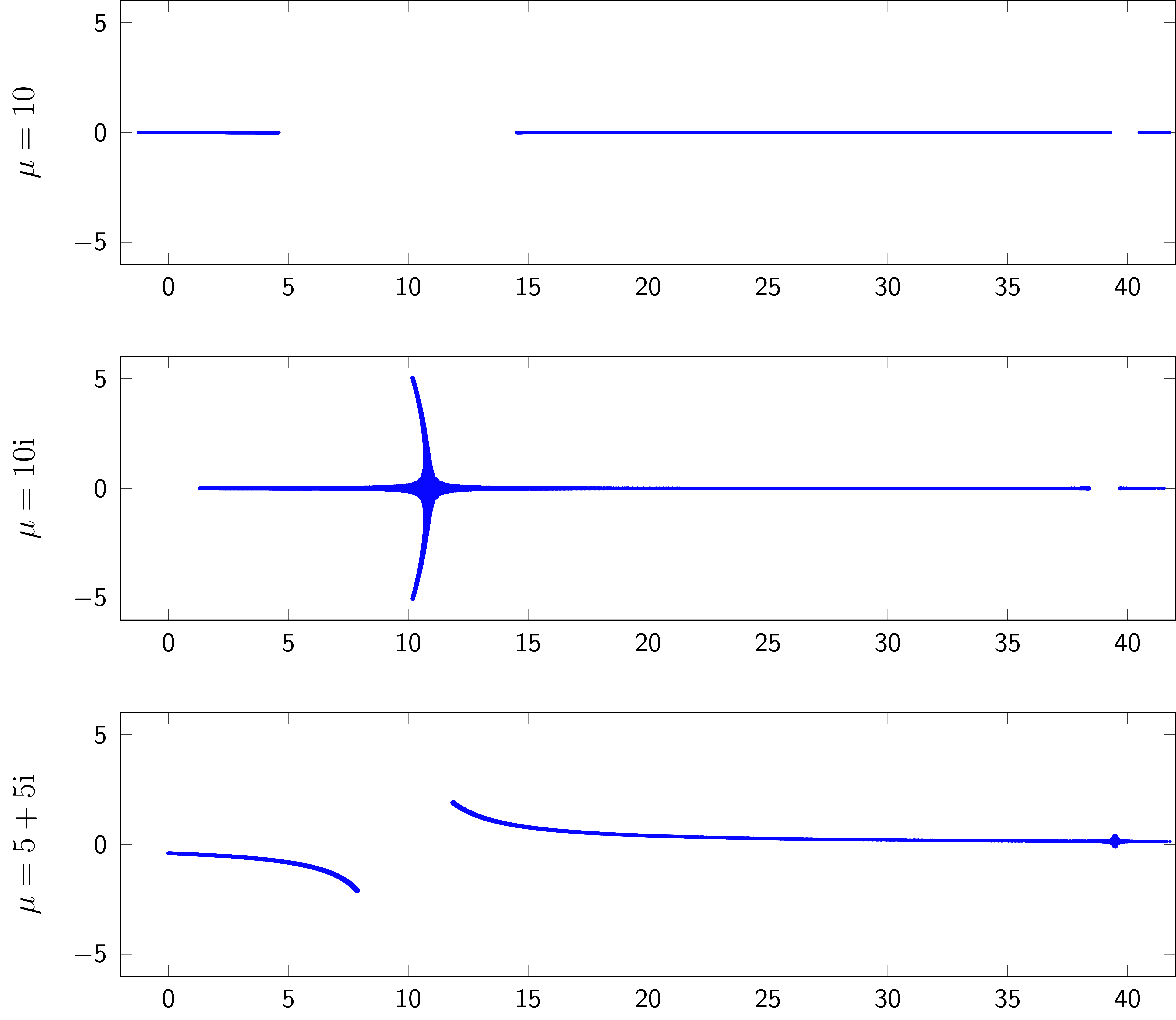
Unten zeigen wir die Ausgabe unseres Algorithmus für den Operator $\mathsf{H_\mu}$, angewendet auf drei verschiedene Werte des Parameters $\mathsf\mu$. Unsere Ergebnisse zeigen klar die qualitativen Eigenschaften der obigen Abbildung.
-
[Shin. On the shape of spectra for non-self-adjoint periodic Schrödinger operators. J. Phys. A, 37(34):8287-8291, 2004] ↩︎