Research
Pseudospectra of Non-Hermitian Hamiltonians
Research article:
- Patrick W. Dondl, Patrick Dorey, Frank Rösler; A Bound on the Pseudospectrum for a Class of Non-normal Schrödinger Operators. Appl. Math. Res. Express 2016.
Overview:
This was the first project of my PhD. The work is concerned with the Schrödinger equation with complex-valued potentials. In general, the eigenvalues (or the spectrum) of such operators could be any complex number, however, some potentials exhibit special symmetries (called PT-symmetry), which constrain their eigenvalues to lie on the real axis. An example is the imaginary cubic oscillator, defined as
$$
\mathsf{H = -\frac{d^2}{dx^2} + ix^3} \quad \textsf{ on }\quad \mathsf{L^2(\mathbb R)}
\tag{1}
$$
Indeed, this operator can be shown to be PT-symmetric and its eigenvalues are purely real, as the following numerical plot illustrates.

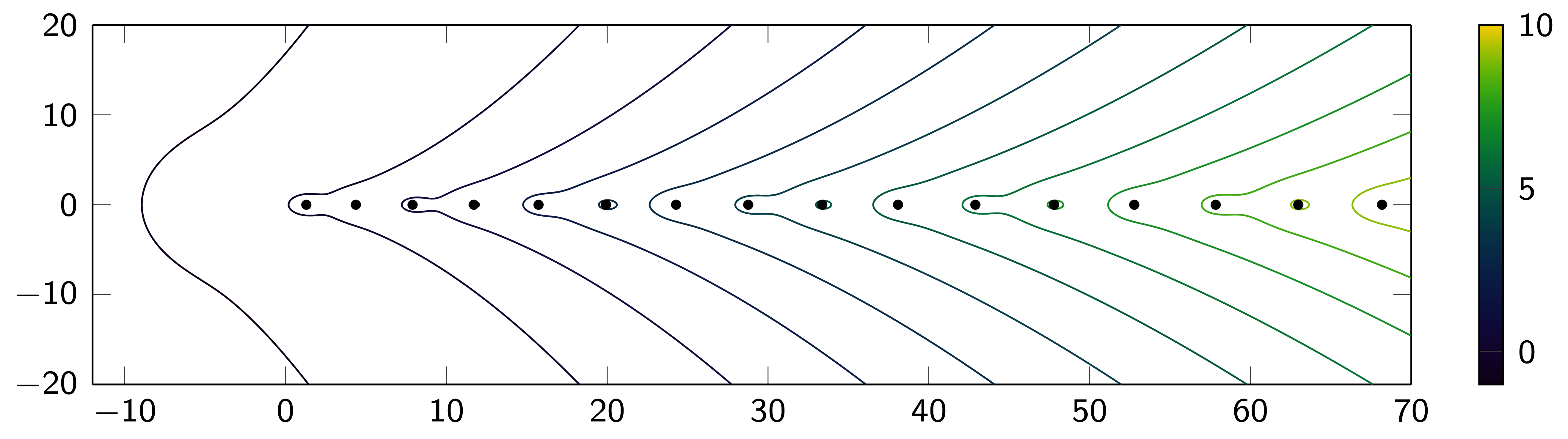
Other examples from the literature show that the pseudospectrum of non-hermitian operators can indeed look arbitrarily chaotic. Our own contribution in the paper mentioned above was to prove that for a class of examples such as the imaginary cubic oscillator the situation is not all bad: Even though the pseudospectrum is not simply given by the distance to the spectrum, we prove certain bounds on $\mathsf{R(z)}$, which imply that on any half plane which extends to the left in the complex plane, the function is determined, to some extent, by the eigenvalues in that half plane. Even though suggested by the numerical figure above, this result is highly nontrivial and not guaranteed except for a very limited class of operators.
-
[Bender, Carl M. Making sense of non-Hermitian Hamiltonians. Reports on Progress in Physics 70.6 (2007): 947.] ↩︎