Research
Computing Bound States in Relativistic Quantum Mechanics
Research article:
- Frank Rösler, Christiane Tretter; Computing Klein-Gordon Eigenvalues, preprint. (supported by the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie grant agreement No 885904.) (A Matlab implementation of the algorithm is available here. A recent presentation on the topic is also available online)
Overview:
The computational spectral problem in quantum mechanics is becoming more and more well understood. Particularly the numerical complexity of the classical (nonrelativistic) theory that goes back to Schrödinger and Heisenberg has been studied in a number of different situations by a number of different authors (including myself and my collaborators), see here, here or here. This has not been the case for the relativistic theory, which is concerned with particles whose velocities approach the speed of light. The underpinning of relativistic quantum mechanics is formed by two equations of motion, the Dirac equation and the Klein-Gordon equation. Either of these equations replaces the classical Schrödinger equation in relativistic settings (depending on whether the particle considered has nonzero spin).
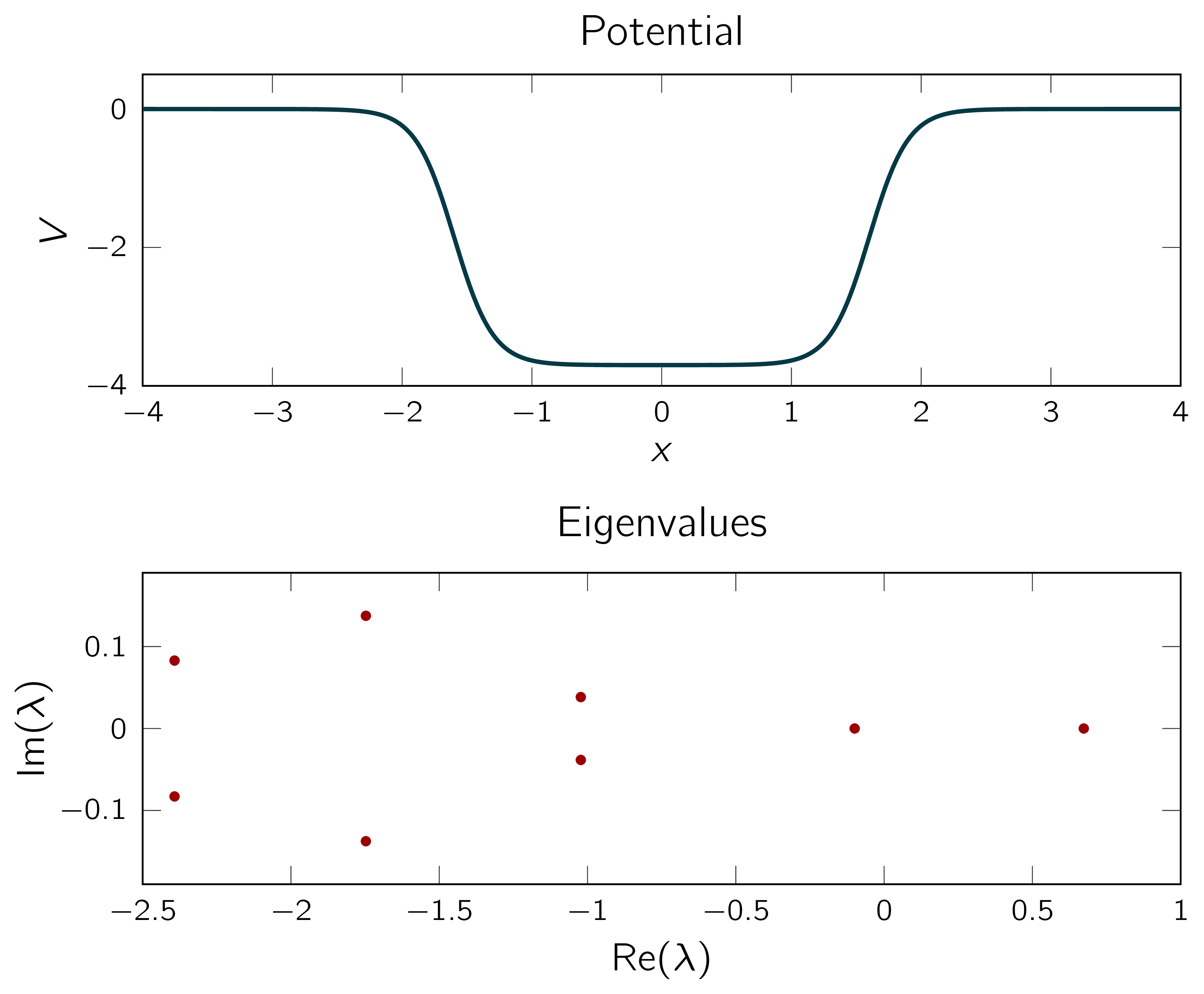
Our new research work above concerns the computation of eigenvalues for the Klein-Gordon equation. This equation governs the evolution of relativistic, spinless particles, most famously the Higgs Boson, which was discovered by the ATLAS and CMS experiments at the Large Hadron Collider (LHC) at CERN and earned Peter Higgs and François Englert a Nobel Prize in Physics in 2013. For a particle of mass $\mathsf{m}$ and charge $\mathsf{e}$, interacting with an electric field $\mathsf{\varphi}$, the equation reads
$$\mathsf{\left( - \Bigl( -i \hbar\frac \partial {\partial t} - e \varphi
\Bigr)^2 - \hbar^2c^2 \Delta + m^2c^4 \right) \psi = 0,}$$
where $\mathsf{c}$ denotes the speed of light and $\mathsf{\hbar}$ is Planck’s constant. If we separate time by setting $\mathsf{\psi(x,t) =: e^{i\lambda/\hbar t} u(x)}$, $\mathsf{x\in\mathbb R^d}$, $\mathsf{t\in\mathbb R}$, normalize $\mathsf{c}$ to $\mathsf{1}$, let $\mathsf{V}$ be the multiplication operator by $\mathsf{e\varphi}$, the above equation simplifies to
$$ \mathsf{(-\Delta+m^2)u = (V-\lambda)^2u. \tag{1}}$$
Solving the above equation amounts to finding a pair $\mathsf{\lambda\in\mathbb C}$, $\mathsf{u\in L^2(\mathbb R^2)}$ such that $(1)$ holds, where $\mathsf V$ is a known function. This problem is reminiscent of the Schrödinger eigenvalue problem, with one major difference: the potential function $\mathsf V$ and the spectral parameter $\mathsf{\lambda}$ enter quadratically, rather than linearly! This renders the problem not only physically, but also mathematically non-classical: one cannot simply transfer results from the nonrelativistic theory, but needs to come up with novel solution techniques.
