Research
Reconstructing a Potential From its Scattering Data
Research article:
- Jonathan Ben-Artzi, Marco Marletta, and Frank Rösler. On the complexity of the inverse Sturm-Liouville problem, Pure and Applied Analysis 5, 895-925 (2023). (supported by the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement No 885904.) (A Matlab implementation of the algorithm is available here)
Overview:
The so-called spectral problem for a Hamiltonian operator $\mathsf{-\frac{d^2}{dx^2}+q}$ consists of finding its spectrum given the potential function $\mathsf q$. In certain cases (e.g. if $\mathsf{q(x)=x^2}$ is the Harmonic Oscillator potential, or the equation is considered on a bounded interval $\mathsf{[a,b]}$), the spectrum is given by the set of eigenvalues, i.e. all points $\mathsf\lambda$ such that $$\mathsf{\bigg(-\frac{d^2}{dx^2}+q\bigg)\psi = \lambda\psi}$$ for some function $\mathsf{\psi\in L^2(\mathbb R)}$, called eigenfunction.
The inverse spectral problem asks the reverse question: can one reconstruct the potential $\mathsf q$ from the spectrum of its Hamiltonian? It turns out that this is indeed possible – if in addition the $\mathsf{L^2}$ norms of the corresponding eigenfunctions are provided. More precisely, if two infinite sequences of numbers $\mathsf{\lambda_n}$, $\mathsf{\|\psi_n\|_{L^2}}$ are given with $$ \mathsf{\lambda_n^{\frac12} \sim n + \frac{\omega}{\pi n}} $$ $$ \mathsf{\frac{1}{\|\psi_n\|_{L^2}^2} \sim \frac{2}{\pi}} $$ as $\mathsf{n\to\infty}$, then the potential $\mathsf q$ is uniquely determined by these sequences.1 The sequences $\mathsf{\lambda_n}$, $\mathsf{\|\psi_n\|_{L^2}}$ are commonly referred to as spectral data.
A more difficult question is whether the function $\mathsf q$ can be computed from these two sequences using a computer algorithm. Since any computer can work only with a finite set of numbers at any given time, one can never recover the potential exactly from the infinite spectral data. Rather, one needs to truncate them and attempt to compute the potential from finite subsequences $\mathsf{\lambda_1,\dots,\lambda_N}$, $\mathsf{\|\psi_1\|_{L^2},\dots,\|\psi_N\|_{L^2}}$. This yields an approximate potnetial $\mathsf{q_N}$, which is expected to converge to the actual potential $\mathsf q$, as $\mathsf{N\to\infty}$.
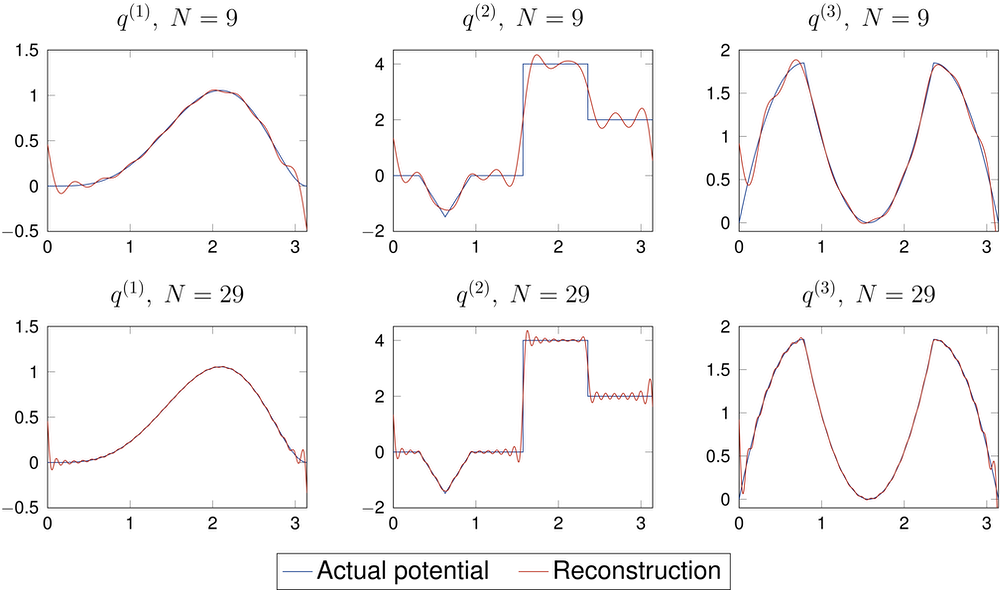
In our research article we study precisely how the potential can be recovered from such finite subsequences and how the approximation error, introduced by the truncation, can be controlled. We explicitly construct a computer algorithm that computes the potential from the truncated spectral data. The figure below shows some example results for three different potentials $\mathsf{q^{(1)}}$, $\mathsf{q^{(2)}}$, $\mathsf{q^{(3)}}$. The first line shows the results of the approximation procedure for a truncation length of $\mathsf{N=9}$, the second line for $\mathsf{N=29}$. As one can see, the approximation improves as $\mathsf N$ is increased.
-
[Freiling-Yurko. Inverse Sturm-Liouville Problems and Their Applications. Nova Science Pub Inc., 2001] ↩︎