Research

Computing the Sound of the Sea in a Seashell

Research article:

  • Jonathan Ben-Artzi, Marco Marletta, Frank Rösler; Computing the Sound of the Sea in a Seashell. Found. Comput. Math., 2021. (supported by the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie grant agreement No 885904.) Click here to download the slides of a recent talk on the subject. A Matlab package based on the article is available here

Overview:

This work considers the scattering of waves by obstacles in 2 dimensions. The mathematical basis for this phenomenon is the Laplacian operator $$\mathsf{H = -\Delta \quad\textsf{ on }\quad \mathbb R^2\setminus U,}$$ where $\mathsf U$ denotes the obstacle and we assume zero boundary conditions on the boundary of $\mathsf U$. If the spatial configuration of the obstacle is such that waves are “almost trapped” (e.g. if $\mathsf U$ has the shape of a chamber), the phenomenon of slowly decaying states (as described in my quantum resonance article) is observed. Scattering resonances of this type can be studied using the same mathematical toolbox as quantum resonances. A well-known model problem which exhibits scattering resonances is the so-called Helmholtz resonator, defined as follows.
Consider a domain $\mathsf{U^\varepsilon\subset\mathbb R^2}$, which is given by a ball $\mathsf {B_r}$ which is connected to the exterior space $\mathsf{\mathbb R^2\setminus B_{R},;R>r}$ by a narrow tube of radius $\mathsf\varepsilon>0$. Any wave which enters the cavity will be almost trapped, because energy can only dissipate through the tube. It has been shown that resonances of this problem are given by points in the complex plane which approach the eigenvalues of the Laplacian on the “closed” chamber $\mathsf {B_r}$ as $\mathsf{\varepsilon\to 0}$.1

In our above article, we devised a computer algorithm that automatically computes the scattering resonances for 2d obstacles of arbitrary shape. The mathematical idea behind the algorithm is to identify the resonances of the obstacle as zeroes of an analytic function, the so-called Dirichlet-to-Neumann map $\mathsf{M(k)}$. This map turns out to admit a $\mathsf{n\times n}$ matrix approximation of the form $\mathsf{I_n+K_n(k)}$, where $\mathsf I$ denotes the identity matrix and $\mathsf{K_n}$ is a convergent sequence of matrix-valued functions. The animation below shows a contour plot of the map $\mathsf{\text{det}(I_n+K_n(k))}$, computed in MATLAB. The red dots indicate the eigenvalues of the Laplacian on the disk $\mathsf{B_r}$. As expected, there are three roots of $\mathsf{\text{det}(I_n+K_n(k))}$ near the three red dots, which move further and further down into the complex plane as the opening width $\mathsf\varepsilon$ increases.

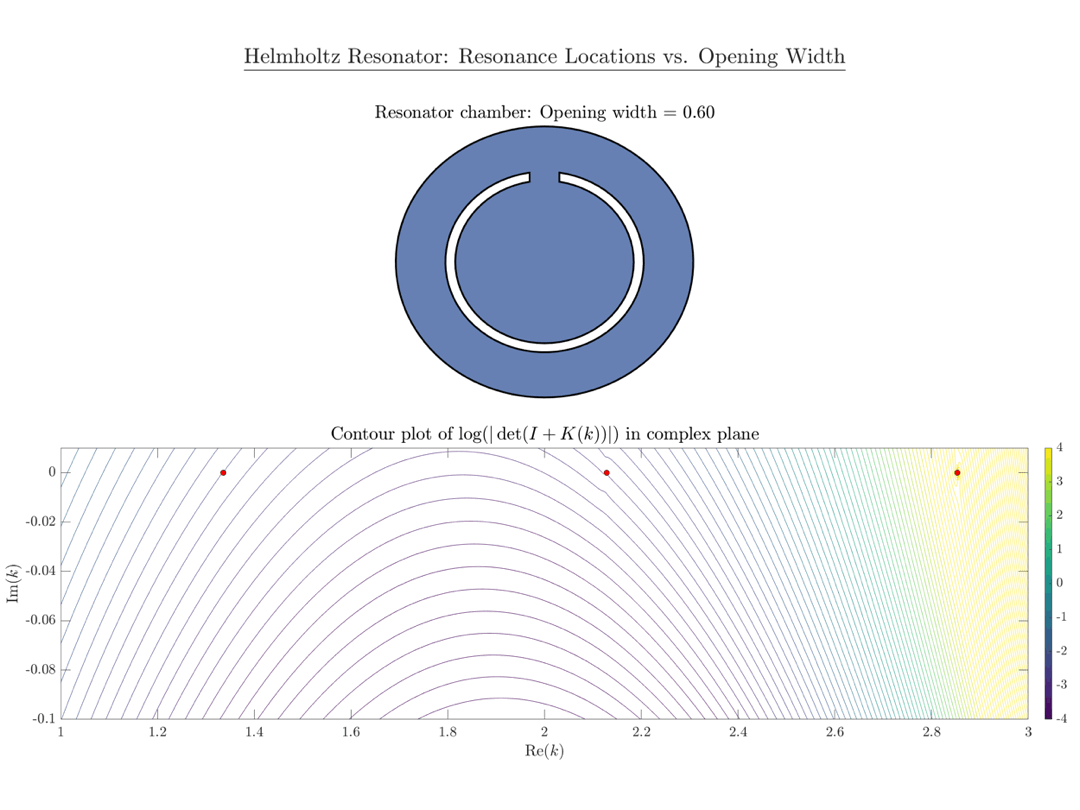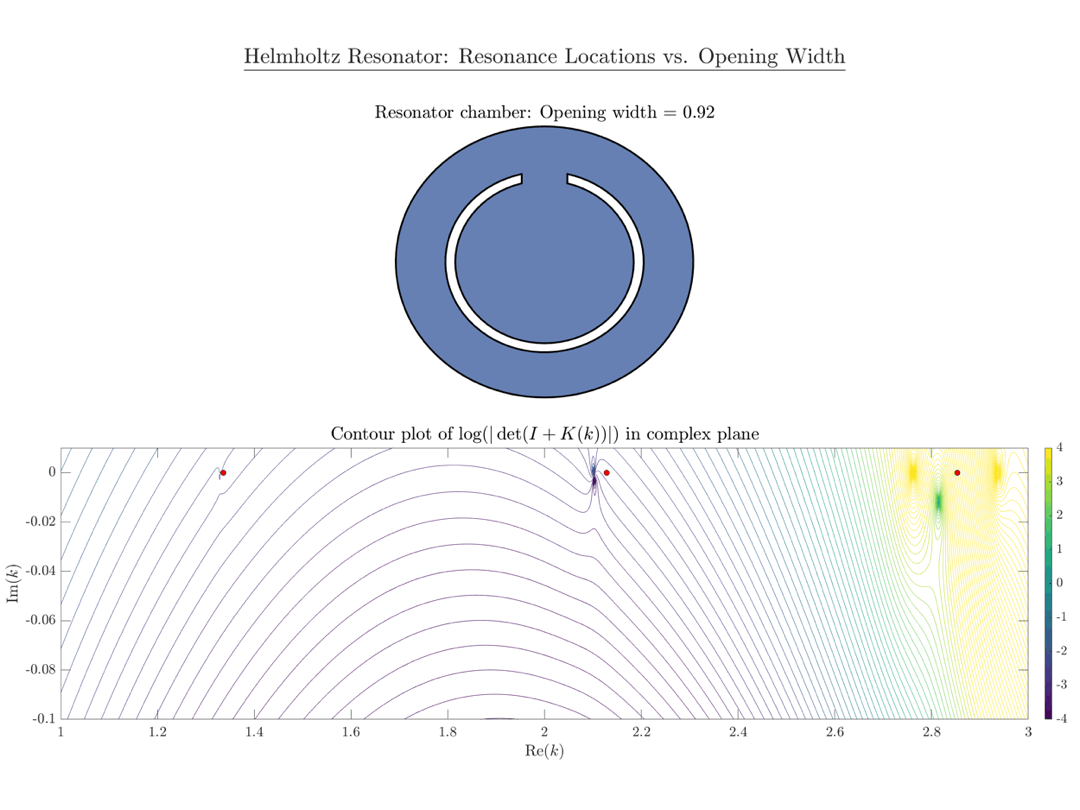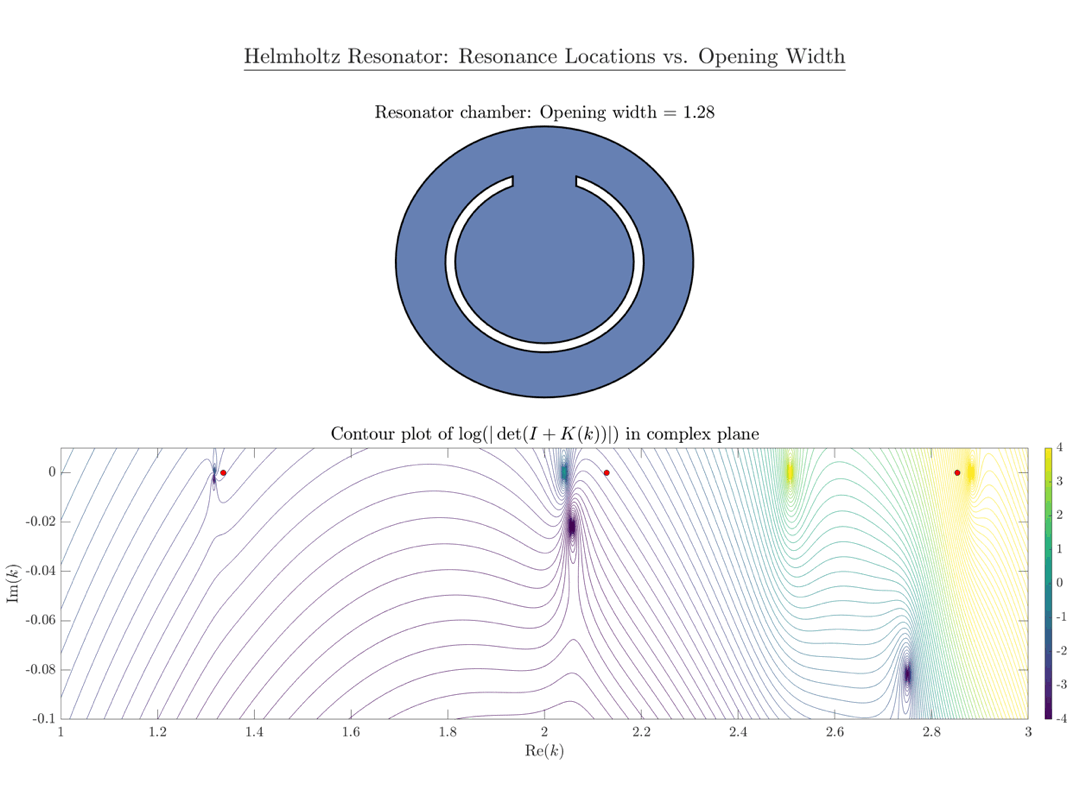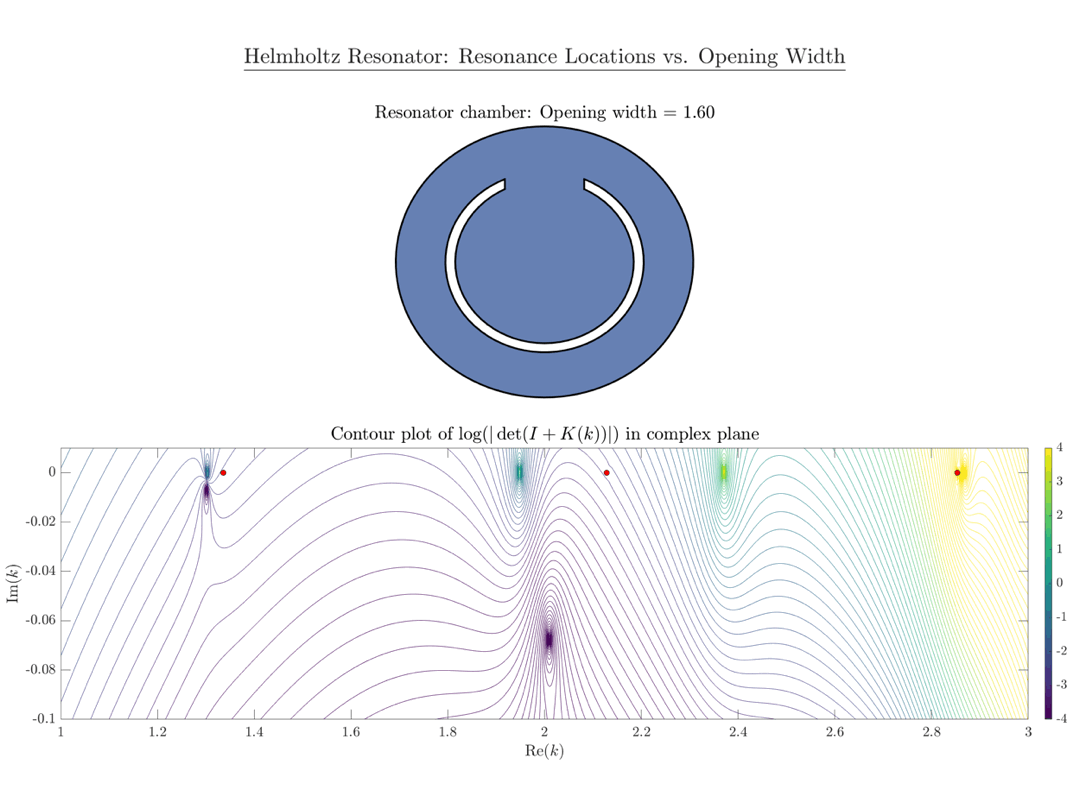
Example image

An implementation in MATLAB based on our work is available on my GitHub page.

  1. [Hislop, P. D., & Martinez, A. (1991). Scattering Resonances of a Helmholtz Resonator. Indiana Univ. Math. J., 767-788.] ↩︎