Hobbyprojekte
Bildrekonstruction via Compressed Sensing
Compressed Sensing ist mittlerweile die State-of-the-Art-Methode zur Bildrekonstruktion aus gemessenen Daten. Ein solches Beispiel sind Röntgen-CT-Messungen und die Radontransformation. Die Hauptidee hinter Compressed Sensing liegt in der Beobachtung, dass die meisten Bilder von Interesse in einer angemessenen Darstellung dünn besetzt (engl. sparse) sind. Dies bedeutet, dass sie deutlich komprimiert werden können, ohne viel Information zu verlieren. Das nächste Bild veranschaulicht dieses Phänomen für die Fourier-Darstellung eines sog. GLPU phantoms. Das Bild auf der rechten Seite enthält genau die selbe Information wie das Bild auf der linken Seite, aber die meisten seiner Pixel sind (fast) 0. Tatsächlich ist es dieses Prinzip, das modernen Bildkompressions-Standards wie JPEG zugrunde liegt.

Nehmen wir als nächstes an, wir hätten einen CT scan durchgeführt und ein Sinogramm $y$ gemessen. Wir wollen das Originalbild aus dem Sinogramm rekonstruieren, wie bereits in einem früheren Post erklärt. Da die Radontransformation linear ist, kann das Rekonstruktionsproblem als Matrixinversion betrachtet werden:
$$Ax=y.\tag{1}$$
Dies wäre auf einem Computer schnell und einfach zu lösen, doch in der Realität stellen sich zwei Probleme: Erstens ist das gemessene Sinogramm typischerweise verrauscht, was die Qualität des rekonstruierten Bildes $x$ beeinträchtigt. Zweitens kann in der Praxis bei einem CT nur eine endliche Anzahl an Winkeln gemessen werden, wodurch das Rekonstruktionsproblem unterbestimmt ist: Es existieren viele Bilder $x$, die das Sinogramm $y$ erzeugen. Tatsächlich sieht Problem (1) also wie folgt aus:
$$Ax + e = y,\tag{2}$$
wobei $e$ das Rauschen repräsentiert und $A$ eine nicht-invertierbare Matrix ist (in aller Regel nichtmal eine quadratische).
Compressed Sensing löst diese beiden Probleme, indem es unter allen möglichen Lösungen $x$ von (2) diejenige Lösung $\hat x$ auswählt, die die “dünnste” Fourier-Darstellung1 hat. Mathematisch bedeutet dies, man löst das Minimierungsproblem
$$\min_{x\in\mathbb{C}^{N\times N}} \Vert\Phi x\Vert_{l^1} \quad \text{sodass} \quad \Vert Ax-y\Vert_{l^2}<\|e\|_{l^2}, \tag{3}$$
wobei (in unserem Fall) $\Phi$ die Fouriertransformation ist. Tatsächlich kann man zeigen, dass die Minimierung der $l^1$-Norm eines Vektors ihn dünn besetzt macht.

In vielen Situationen schneidet Compressed Sensing besser ab, als die klassische Rekonstruktion mittels inverser Radontransformation (auch als “filtered backprojection” bekannt). Das nächste Bild zeigt einen Vergleich zwischen Rekonstruktion mit Compressed Sensing (links) und klassischer inverser Radontransformation (rechts) aus einem stark verrauschten Sinogramm. Wie man sieht, hat die Rekonstruktion mittels Compressed Sensing hier eine deutlich höhere Bildqualität.
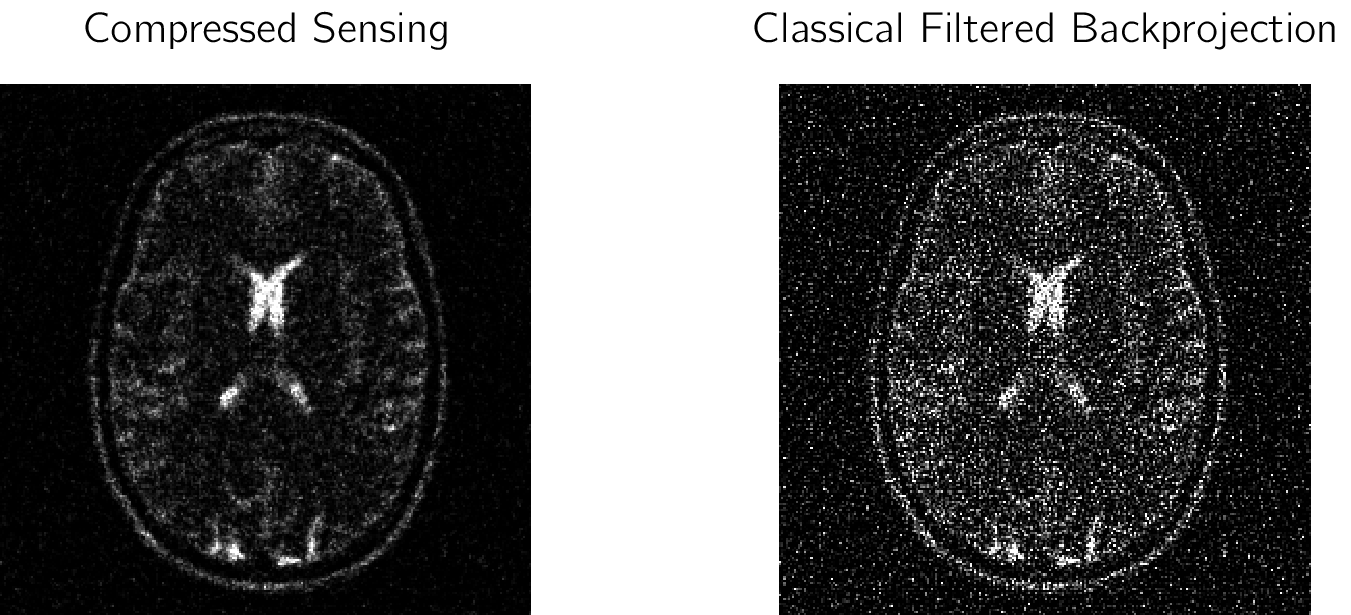
Die obigan Bilder stammen aus meinen eigenen Implementierungen des Algorithmus. Versionen in MATLAB und Python sind auf meiner GitHub-Seite verfügbar: https://github.com/frank-roesler/compressed_sensing.
-
Fourier ist keinesfalls die einzig mögliche Wahl hier. Viele andere “sparsifying” Transformationen sind denkbar. Eine beliebte Alternative ist z.B. die Wavelet Transformation. ↩︎