Hobbyprojekte

Modellierung von MRT-Pulsen

Kernspinresonanz

In der Magnetresonanztomographie (MRT) werden die Spins der Atomkerne in unserem Körper in ein starkes homogenes Magnetfeld $\mathsf{B_0}$ gebracht und durch einen Radiofrequenzpuls (RF) angeregt. Nach der Anregung rotieren die Spins gemeinsam in Phase und produzieren eine messbare makroskopische Magnetisierung $\mathsf{M(t)}$, die in der Zeit nach dem RF-Puls wieder zerfällt. Dieses messbare Signal wird in der MRT als “free induction decay” (FID) bezeichnet. Die Form des RF-Pulses ist zentral für die Kontrolle des angeregten Frequenzbereichs. Besonders wichtig ist die Fähigkeit, einen spezifischen, schmalen Frequenzbereich anzuregen. Tatsächlich ist dies zwingend notwendig, um die räumliche Information zu gewinnen, die letztendlich zu medizinisch nützlichen Bildern führt.
Allerdings ist die Beziehung zwischen Form des RF-Pulses und der entsprechenden Frequenzantwort alles andere als einfach. Sie kann mathematisch modelliert werden durch die sogenannten Bloch-Gleichungen:

$$\mathsf{\frac{d M_x(t)}{dt} = -\Delta\omega M_y(t) - \gamma B_{1,y}(t)M_z(t) - \frac{M_x(t)}{T_2} }$$ $$\mathsf{\frac{d M_y(t)}{dt} = \Delta\omega M_x(t) + \gamma B_{1,x}(t)M_z(t) - \frac{M_y(t)}{T_2} }$$ $$\mathsf{\frac{d M_z(t)}{dt} = \gamma B_{1,y}(t)M_x(t) - \gamma B_{1,x}(t)M_y(t) - \frac{M_z(t) - M_z^0}{T_1} }.$$

Hierbei bezeichnet $\gamma$ eine physikalische Konstante, das gyromagnetische Verhältnis und $\mathsf{B_1}$ das Magnetfeld des angelegten RF-Pulses. $\mathsf{\Delta\omega}$ bezeichnet die Abweichung von der Larmorfrequenz des Gewebes. Idealerweise sollte ein RF-Puls in der Lage sein, die Komponenten $\mathsf{M_x}$, $\mathsf{M_y}$, $\mathsf{M_z}$ nur in einem schmalen Bereich um $\mathsf{\Delta\omega=0}$ anzuregen.

Numerische Modellierung

Die Bloch-Gleichungen lassen sich numerisch lösen. Eine der gängigen Lösungsmethoden habe ich in Python implementiert. Sie ermöglicht sowohl ein qualitatives, als auch ein quantitatives Verständnis von MRT-Sequenzen. Der Code ist open source und auf github.com/frank-roesler/bloch_solver frei verfügbar. Die folgende Grafik illustriert den Effekt eines sinc-förmigen RF-Pulses auf die Magnetisierung $\mathsf M$ für $\mathsf{\Delta\omega=0}$. Die Komponente $\mathsf{M_y}$ wird nach jedem Puls angeregt, wonach sie exponentiell zerfällt. Man beachte, dass der erste Puls (etwa zur Zeit 200ms) eine maximale Anregung erreicht (d.h. $\mathsf{M_y}=1$), wobei alle folgenden Pulse aufgrund der unvollständigen $\mathsf T_1$-Regeneration nur eine teilweise Anregung erreichen. Dies ist genau das Verhalten, das man theoretisch erwartet und in Messungen sieht. (siehe z.B. hier).

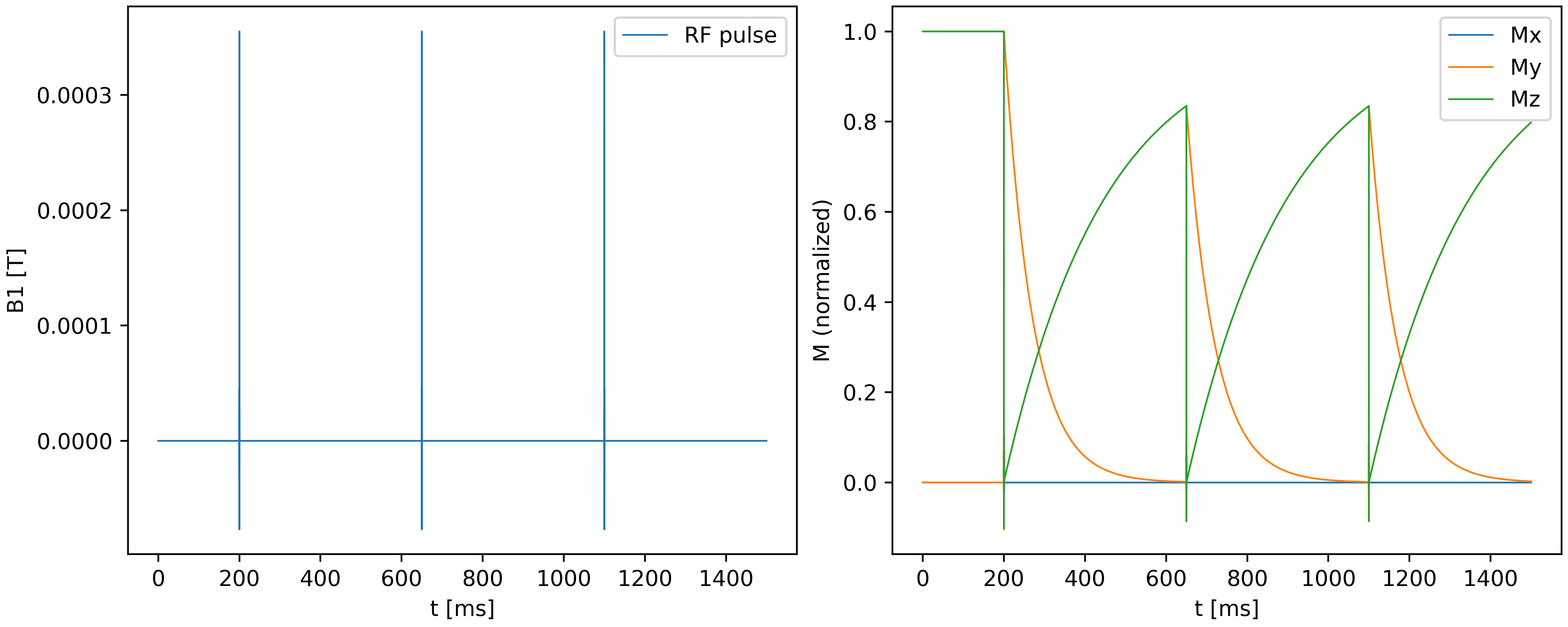
Spin Echo und Feldgradienten

Der Python-Code ermöglicht auch die qualitative Illustration von komplexeren MRT-Sequenzen. Die meisten modernen Sequenzen nutzen einen Effekt namens “Spin Echo”. Dieser Effekt erlaubt es, den $\mathsf{T_2}$-Zerfall teilweise umzukehren, indem man RF-Pulse und magnetische Feldgradienten clever kombiniert. Die zentrale Idee besteht darin, die Spins, die durch ein inhomogenes Magnetfeld außer Phase geraten sind, wieder in eine Linie zu bringen. Dies kann entweder durch einen sogenannten 180º RF-Puls erreicht werden, oder durch zwei entgegengesetzte Feldgradienten. Das folgende Bild illustriert den ersten Fall. Ein erster Puls regt die Magnetisierung an, wonach sie durch Inhomogenitäten im Magnetfeld (hier einfachheitshalber modelliert durch einen konstanten Gradienten) wieder zerfällt. Nach einer Zeit $\mathsf{T_E/2}$ wird ein weiterer Puls (der 180º-Puls) angelegt. Die Numerik zeigt einen zweiten Peak in der Magnetisierung (orange), der zur Zeit $\mathsf{T_E}$ scheinbar aus dem Nichts entsteht. Dies wird in der MRT als “Spin-Echo bezeichnet”.

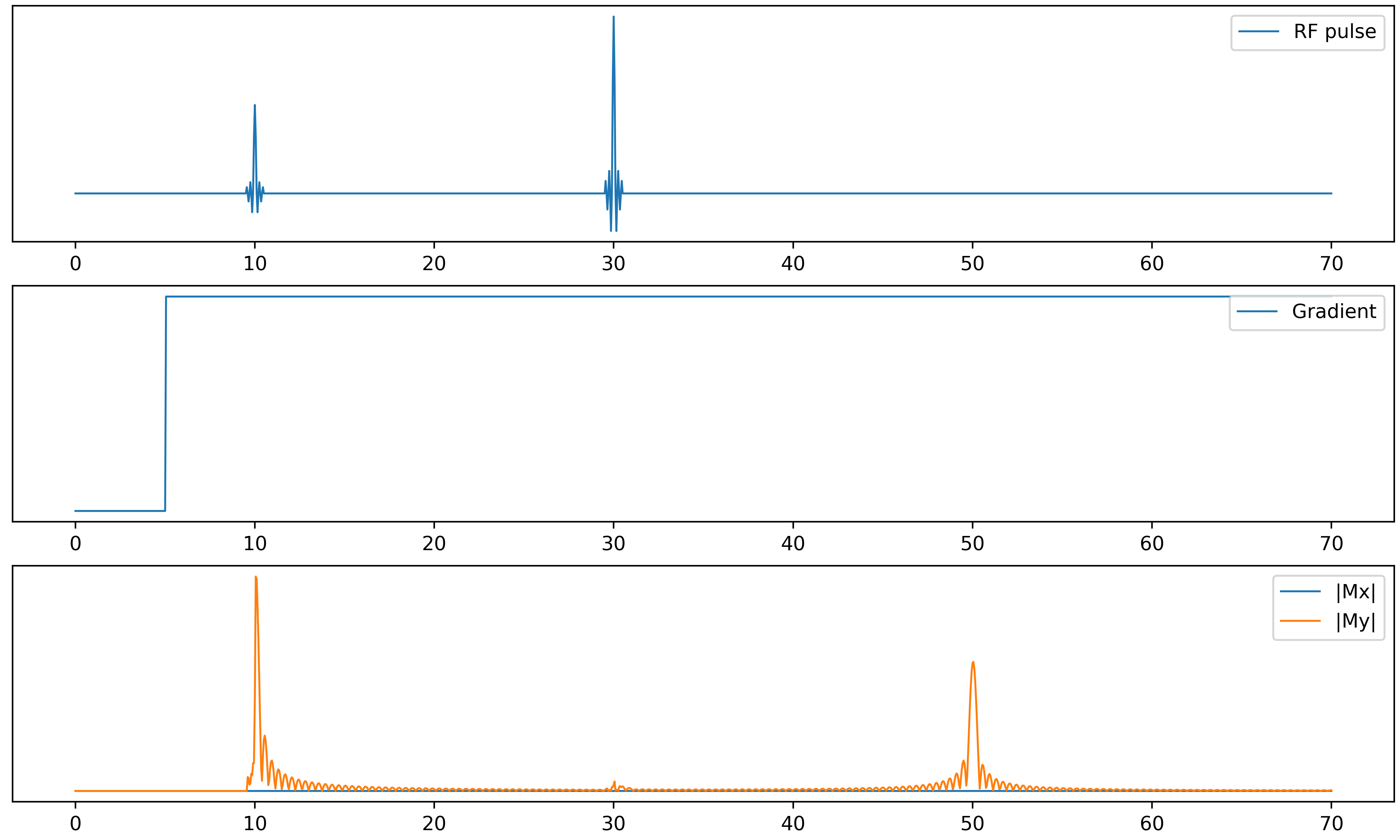
Der zweite Fall, das “Gradientenecho”, ist im letzten Bild unten illustriert. Anstatt eines zweiten RF-Pulses wird hier ein magnetischer Feldgradient angelegt, erst in positive Richtung, dann in negative. Der erste (positive) Gradient verursacht eine Dephasierung der Spins, welche zu rapidem Signalverlust führt. Der zweite (negative) Gradient kehrt diesen Effekt um, verursacht also eine Rephasierung. Wie erwartet, kehrt das Signal während des zweiten Gradienten zurück (orangener Peak).

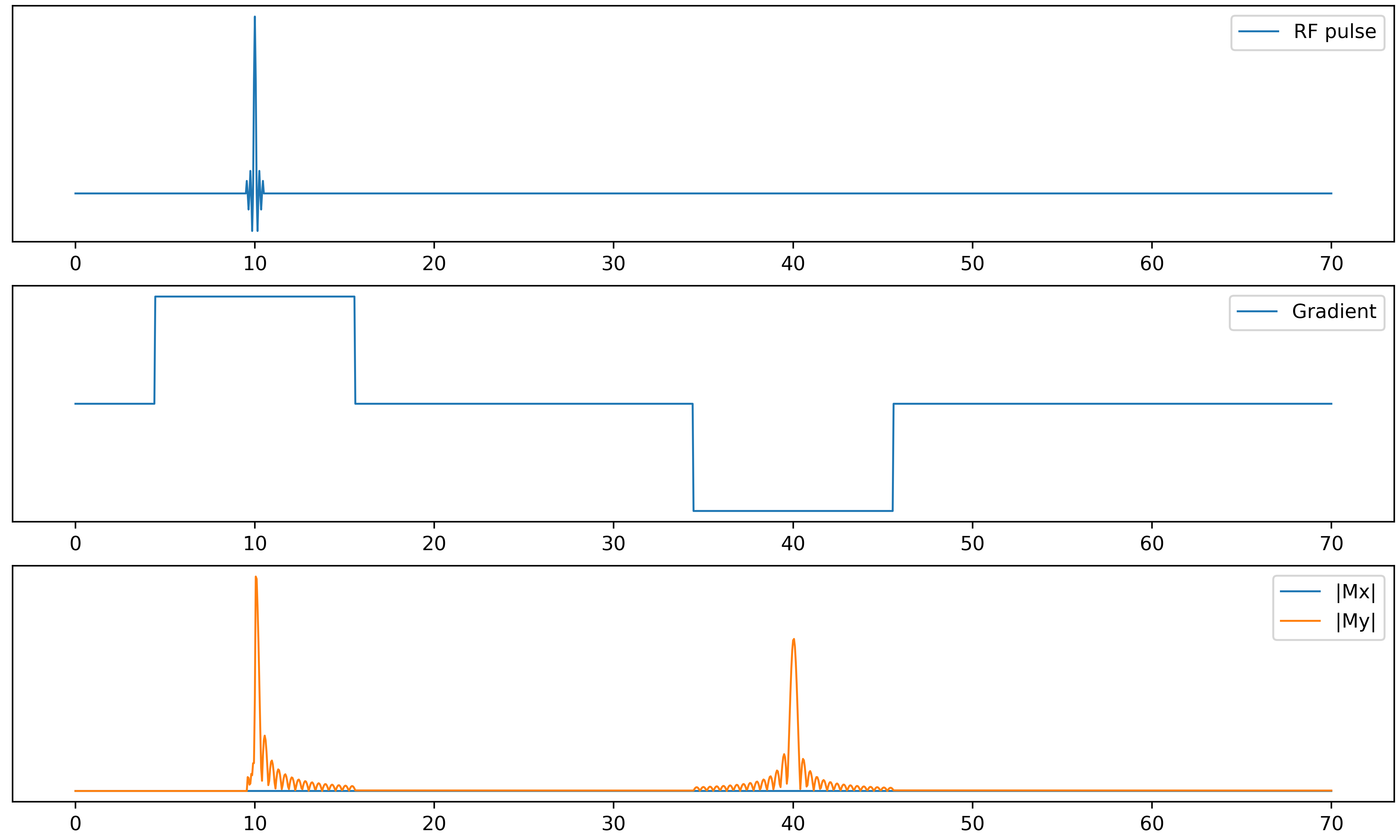
All diese Effekte lassen sich an einem MRT-Gerät tatsächlich experimentell beobachten. Die Bloch-Gleichungen (zusammen mit ein bisschen Numerik) erlauben es uns, sie zu verstehen und vorherzusagen und alles, was wir dazu benötigen, ist ein Laptop!