Hobby Projects
Image Reconstruction via Compressed Sensing
Compressed Sensing is now the state-of-the-art method in many applications that require images to be reconstructed from measured data. One such example is given by X-Ray CT measurements and the Radon transform.
The main idea behind the compressed sensing method is to exploit the fact that most images of interest are sparse in an appropriate representation, meaning that they can be compressed significantly without losing much information. The following figure illustrates this phenomenon using the Fourier representation of the so-called GLPU phantom image. The image on the right-hand side contains exactly the same amount of information as the image on the left hand side, yet most pixels on the right hand side are almost zero. This principle, in fact, underlies modern image compression standards like JPEG.

Suppose now that we have performed a CT scan and measured a sinogram $y$. We would like to reconstruct the original image from the sinogram, as I explained in an earlier post. Since the Radon transform is linear, the reconstruction problem can be considered as a matrix inversion problem $$Ax=y.\tag{1}$$ In practice, however, one faces two challenges: first, the measured sinogram is typically noisy, which generally reduces the quality of the reconstruction. Second, the fact that only a finite number of angles can be measured means that the reconstruction problem is underdetermined: there are generally many images $x$ that produce the sinogram $y$. Accordingly, problem (1) is modified into $$Ax + e = y,\tag{2}$$ where $e$ represents the noise and $A$ is a non-invertible matrix (typically not even a square matrix). Compressed sensing tackles these issues by considering all possible solutions $x$ to (2) and choosing the unique one $\hat x$ with the sparsest Fourier representation.1 Mathematically, this amounts to solving the minimization problem $$\min_{x\in\mathbb{C}^{N\times N}} \Vert\Phi x\Vert_{l^1} \quad \text{subject to} \quad \Vert Ax-y\Vert_{l^2}<\|e\|_{l^2}, \tag{3}$$ where (in our case) $\Phi$ denotes the Fourier transform. In fact, it can be shown that minimizing the $l^1$ norm of a vector promotes its sparsity.

In many situations, compressed sensing can outperform the classical reconstruction via filtered backprojection. The following figure shows a comparison between compressed sensing (left) and filtered backprojection (right) in the presence of strong Gaussian noise $e$. As can be seen, the reconstruction via compressed sensing has substantially higher quality.
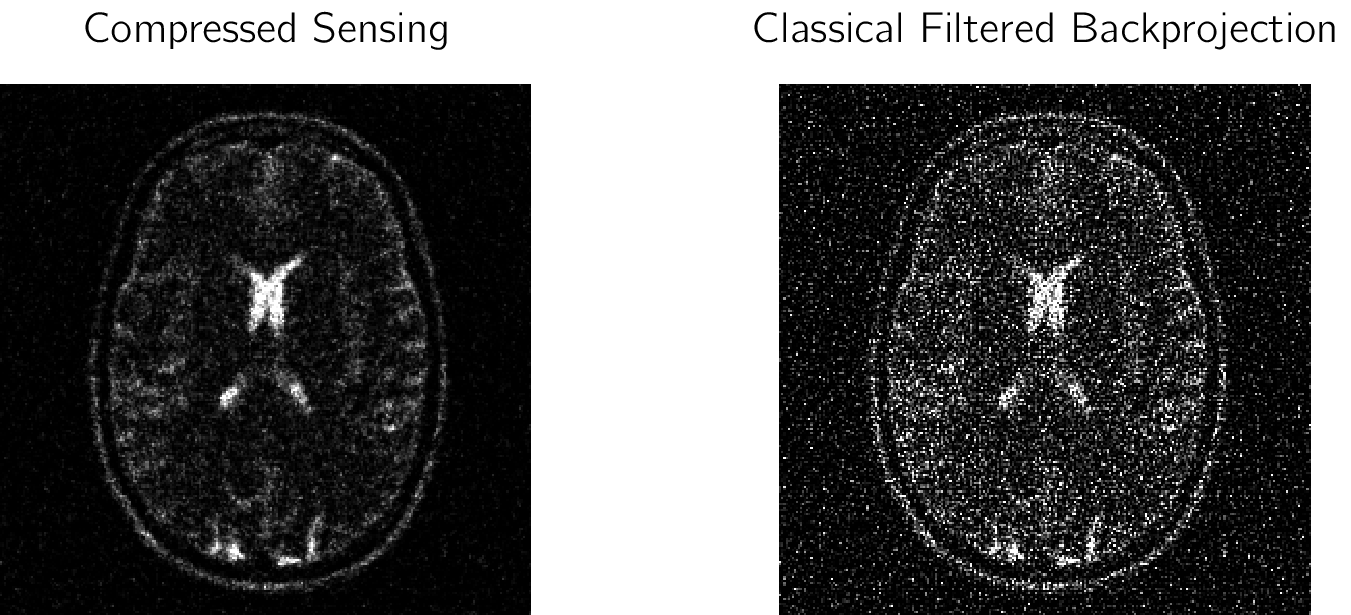
The images presented above are from my own implementations of the algorithm. Example codes in both MATLAB and Python are available at https://github.com/frank-roesler/compressed_sensing.
-
Fourier is by no means the only reasonable chioce here. Many other unitary sparsifying transforms can be used instead. A popular alternative choice is the Wavelet transform. ↩︎