Hobby Projects

Deep Learning for MRI Pulse Sequences

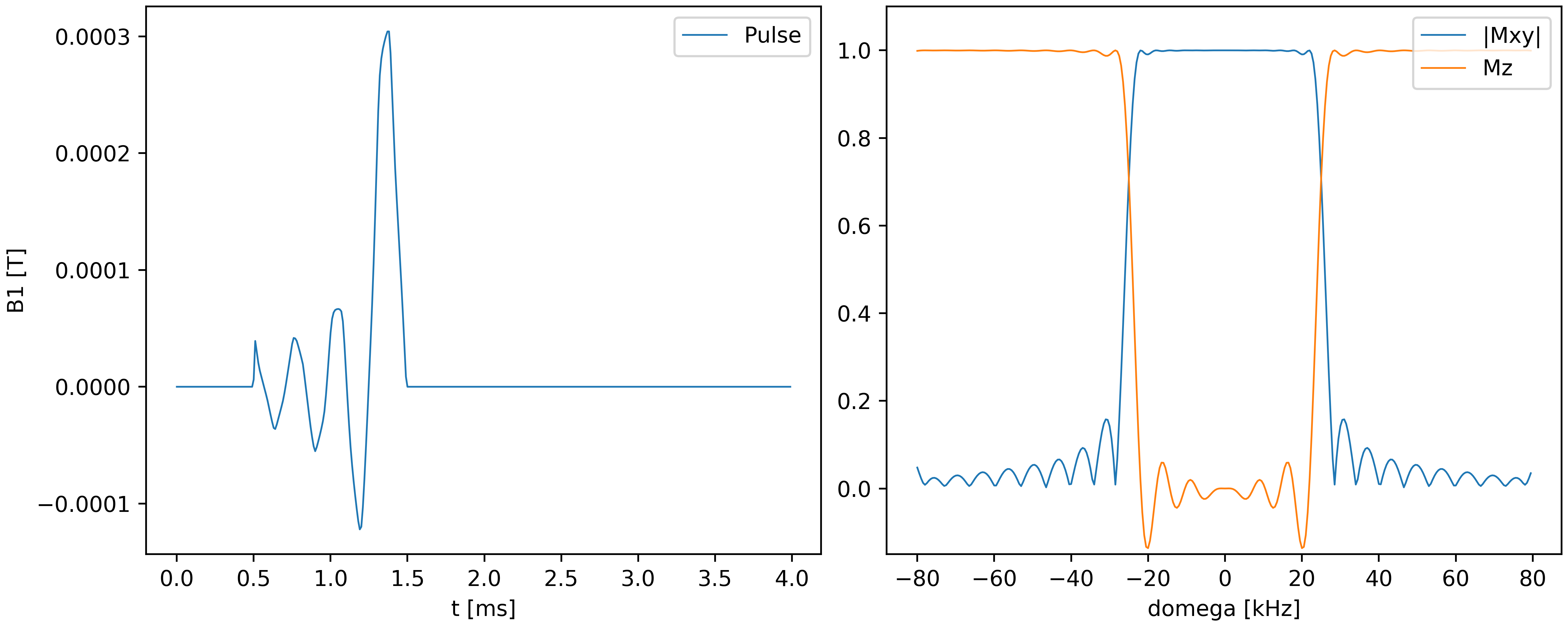
Frequency profile of RF pulse

As explained in this post, the excitation response of nuclear spins with respect to a radiofrequency (RF) pulse is modeled by the Bloch equations, which can be solved numerically. The frequency profile excited by a given pulse can be obtained by solving the equations for a range of values of $\mathsf{\Delta\omega}$ around 0. It is often desired (e.g. for slice selection) to have a pulse, which excites a rectangular frequency profile of a certain width $\delta$. That is, only frequencies in the range $\mathsf{\Delta\omega\in [-\delta,+\delta]}$ are to be selectively excited uniformly. Heuristically, pulse shapes can be found, which approximately achieve this. One prominent shape is the sinc pulse, given by $\mathsf{B_{1,x}(t)\sim sin(t)/t}$. The following figure shows the frequency profile corresponding to a sinc pulse. As can be seen, it is approximately rectangular, but not perfect.

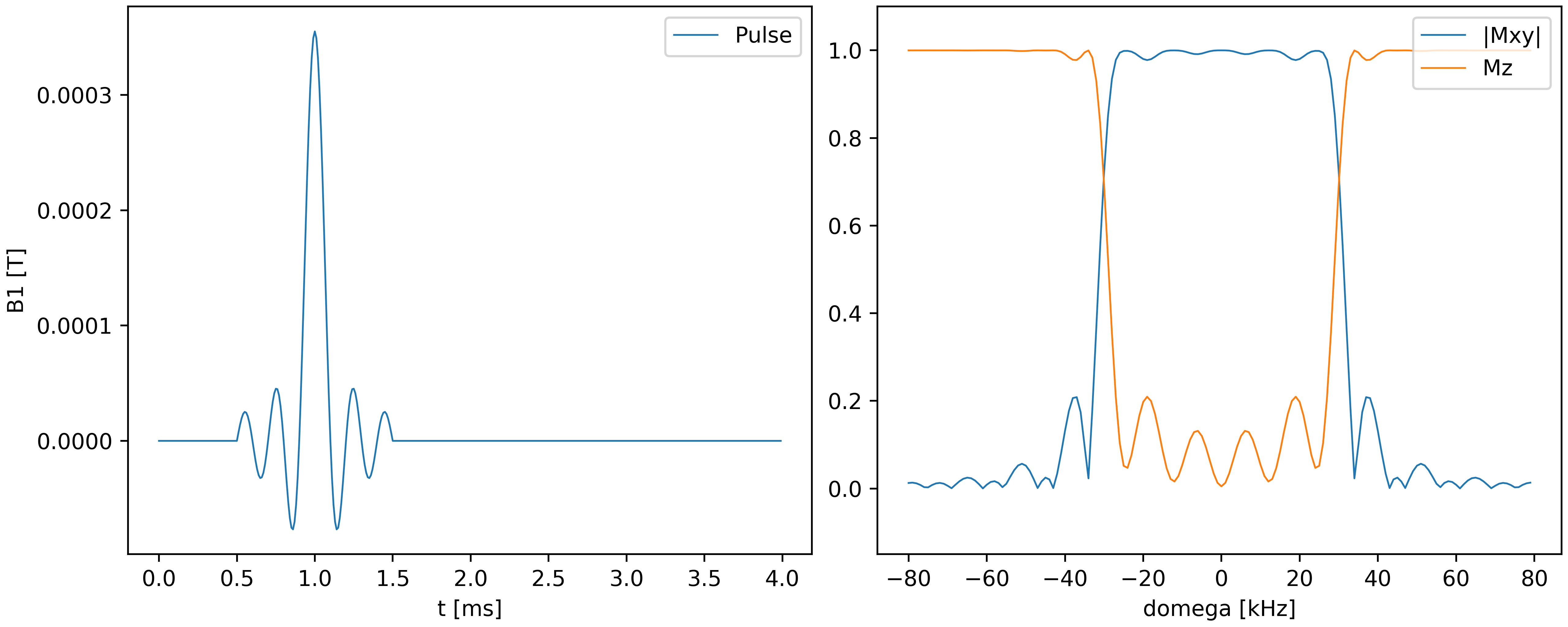
Deep Learning yields new pulse shapes

The task of finding new pulse shapes that better approximate a rectangular profile is highly non-trivial. One possible solution to this issue is provided by machine learning with artificial neural networks:
The process of adapting a pulse shape to better match a specific frequency profile can be understood as training a model function. A neural network turns out to be a natural choice for such a model function, since it can approximate pretty much any shape. Furthermore, neural nets can be trained efficiently, even on personal laptops. The figure below shows a pulse shape obtained by training a neural network, together with its frequency profile. The improvement is apparent.